A B. 4395. feladat (2011. november)

B. 4395. Adott egy húrnégyszög. Szerkesszünk minden oldal belsejében egy-egy pontot úgy, hogy az ezek által meghatározott konvex négyszög kerülete a lehető legkisebb legyen.

(5 pont)

A beküldési határidő 2011. december 12-én LEJÁRT.

Megoldás. A négyszög csúcsait jelölje negatív (óramutató járásával ellentétes) forgásirányban $\displaystyle A,B,C,D$, szögeit értelemszerűen $\displaystyle \alpha, \beta, \gamma, \delta$. Feltehetjük, hogy $\displaystyle \alpha,\beta\ge 90^\circ$.

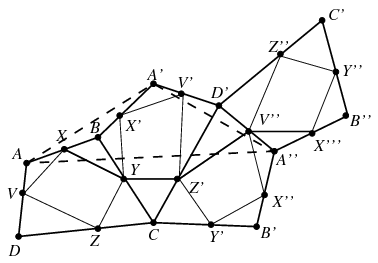
A négyszöget a $\displaystyle BC$ oldal egyenesére tükrözve kapjuk az $\displaystyle A'BCD'$ négyszöget. Ezt a $\displaystyle CD'$ oldal egyenesére tükrözve az $\displaystyle A''B'CD'$ négyszöghöz, végül azt a $\displaystyle D'A''$ oldal egyenesére tükrözve az $\displaystyle A''B''C'D'$ négyszöghöz jutunk. Az $\displaystyle ABCD$ négyszögbe rajzolt $\displaystyle XYZV$ négyszög a tükrözések hatására előbb az $\displaystyle X'YZ'V'$, majd az $\displaystyle X''Y'Z'V''$, végül pedig az $\displaystyle X'''Y''Z''V''$ négyszögbe kerül. A $\displaystyle XYZV$ négyszög kerülete tehát megegyezik az $\displaystyle XYZ'V''X'''$ töröttvonal hosszával, ami legalább akkora, mint az $\displaystyle XX'''$ szakasz hossza.

Az $\displaystyle AB$ félegyenest $\displaystyle 180^\circ$-os forgatás viszi a $\displaystyle BA$ félegyenesbe. $\displaystyle BA$ félegyenest $\displaystyle 2\beta$ szögű forgatás viszi a $\displaystyle BA'$ félegyenesbe. Ezt $\displaystyle 180^\circ$-os forgatás viszi az $\displaystyle A'B$ félegyenesbe, amit $\displaystyle \alpha$ szögű fordatás visz az $\displaystyle A'D'$-be. Ezt $\displaystyle 180^\circ$-os forgatás viszi a $\displaystyle D'A'$ félegyenesbe, amit $\displaystyle 2\delta=360^\circ-2\beta$ szögű forgatás visz a $\displaystyle D'A''$ félegyenesbe (itt használjuk ki, hogy a négyszög húrnégyszög). Végül a $\displaystyle D'A''$ félegyenest $\displaystyle 180^\circ$-os forgatás viszi az $\displaystyle A''D'$ félegyenesbe, amit $\displaystyle -\alpha$ szögű forgatás visz az $\displaystyle A''B''$-be. Ez azt jelenti, hogy az $\displaystyle A''B''$ félegyenes iránya megegyezik az $\displaystyle AB$ félegyenesével, tehát $\displaystyle \overrightarrow{AA''}=\overrightarrow{BB''}=\overrightarrow{XX'''}$. Megállapíthatjuk tehát, hogy az $\displaystyle XX'''$ szakasz hossza független az $\displaystyle X$ pontnak az $\displaystyle AB$ szakaszon elfoglalt helyzetétől.

Tegyük fel, hogy az $\displaystyle XX'''$ szakasz metszi a $\displaystyle BC, CD', D'A''$ szakaszokat. Ekkor az $\displaystyle Y,Z,V$ pontok megválaszthatók oly módon, hogy az $\displaystyle Y,Z',V''$ pontok rendre ezekkel a metszéspontokkal essenek egybe. Világos, hogy ebben az esetben az $\displaystyle XYZV$ négyszög kerülete a lehető legkisebb lesz. Ha viszont ez nem teljesül, akkor az $\displaystyle XYZ'V''X'''$ töröttvonal hossza csak úgy lehet a lehető legkisebb, ha valamelyik töréspont csúcspontba esik. Könnyű meggondolni, hogy ekkor azon $\displaystyle XYZV$ négyszögek közül, melyeknek $\displaystyle X$ csúcsa rögzített, a többi pedig a megfelelő oldalak belsejébe esik, nem lesz legkisebb kerületű, hiszen az ilyen négyszögek kerülete a legrövidebb töröttvonal hosszát tetszőlegesen megközelítheti ugyan, de el nem érheti. Vagyis ha nem található az $\displaystyle AB$ oldal belsejében a fenti tulajdonsággal rendelkező $\displaystyle X$ pont, akkor a feladatnak nincsen megoldása.

A megoldhatóságnak tehát nyilvánvalóan szükséges feltétele, hogy az $\displaystyle ABB''A''$ paralelogramma körüljárása is negatív irányú legyen, vagyis hogy az $\displaystyle A''AA'$ (irányított) szög a $\displaystyle BAA'$ szögnél nagyobb legyen. Az $\displaystyle AA'B$ egyenlőszárú háromszögben a $\displaystyle B$-nél lévő szög $\displaystyle 360^\circ-2\beta=2\delta$, tehát $\displaystyle BAA'\sphericalangle=90^\circ-\delta$. Ehhez hasonló az $\displaystyle A''A'D'$ háromszög, a hasonlóság aránya pedig $\displaystyle AD:AB$, vagyis az $\displaystyle A'A$ szakaszt ilyen arányú, $\displaystyle \alpha$ szögű forgatva nyújtás viszi az $\displaystyle A'A''$ szakaszba. Látható tehát, hogy az $\displaystyle A''AA'$ háromszög hasonló a $\displaystyle DBA$ háromszöghöz, tehát $\displaystyle A''AA'\sphericalangle=ABD\sphericalangle=ACD\sphericalangle$. Az $\displaystyle A''AA'\sphericalangle> BAA'\sphericalangle$ feltétel tehát egyenértékű az $\displaystyle ACD\sphericalangle >90^\circ-CDA\sphericalangle$ feltétellel, vagyis a $\displaystyle DAC\sphericalangle<90^\circ$ feltétellel, ami $\displaystyle \alpha,\beta\ge 90^\circ$ mellett pontosan azt jelenti, hogy a körülírt kör középpontja a négyszög belsejébe esik.

Most megmutatjuk, hogy ezen feltétel teljesülése esetén az $\displaystyle AA''$ szakasz, esetleg a $\displaystyle C$ pont érintésével, végig az ábrán belül halad. Ehhez csak annyit kell ellenőrizni, hogy az $\displaystyle AA'$ szakasz a $\displaystyle BC$ egyenest a $\displaystyle BC$ szakaszon metszi, vagyis hogy $\displaystyle CAB\sphericalangle\ge A'AB\sphericalangle$. Mivel $\displaystyle A''AB\sphericalangle=A''AA'\sphericalangle-BAA'\sphericalangle=90^\circ-DAC\sphericalangle$, ez ekvivalens azzal, hogy $\displaystyle \alpha=DAC\sphericalangle+CAB\sphericalangle\ge 90^\circ$, ahogyan azt kezdetben feltettük. Hasonlóképpen igazolható az is, hogy a $\displaystyle BB''$ szakasz, esetleg a $\displaystyle D'$ pont érintésével, végig az ábrán belül halad; ez ugyanis ekvivalens a $\displaystyle \beta\ge 90^\circ$ feltevéssel. Ekkor viszont az $\displaystyle X$ pont tetszőleges választása esetén teljesülni fog, hogy az $\displaystyle XX'''$ szakasz metszi a $\displaystyle BC, CD', D'A''$ szakaszokat.

Összefoglalva, a feladatnak pontosan akkor van megoldása, ha a körülírt kör középpontja a négyszög belsejébe esik. Ekkor a feladatnak végtelen sok megoldása van, melyek a következő eljárással kaphatók meg. Szerkesszük meg az $\displaystyle A',B,C,D,A'',B''$ pontokat az ábrának megfelelően. Az $\displaystyle AB$ szakasz tetszőleges $\displaystyle X$ belső pontját kijelölve, az $\displaystyle AA''$-vel $\displaystyle X$-en át húzott párhuzamos a $\displaystyle BC,CD',D'A''$ szakaszokat elmetszi az $\displaystyle Y,Z',V''$ pontokban. Innen a $\displaystyle V',Z,V$ pontok tükrözésekkel megkaphatók, és így létrejön egy $\displaystyle XYZV$ négyszög, ami megoldása a szerkesztési feladatnak.

Statisztika:

34 dolgozat érkezett.
5 pontot kapott:	Ágoston Tamás, Barna István, Havasi 0 Márton, Medek Ákos, Mester Márton, Strenner Péter, Szász Dániel Soma, Viharos Andor.
4 pontot kapott:	Beleznay Soma, Maga Balázs, Nagy-György Pál, Schultz Vera Magdolna, Somogyvári Kristóf, Weisz Ambrus.
3 pontot kapott:	11 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2011. novemberi matematika feladatai