A B. 4460. feladat (2012. május)

B. 4460. Megrajzoljuk az ABC háromszög oldalaira kifelé az ABD, BCE és CAF szabályos háromszögeket. Jelölje a BD és BE szakasz felezőpontját rendre G, illetve H, a CAF háromszög középpontját pedig I. Igazoljuk, hogy az AH, CG és BI egyenesek egy pontban metszik egymást.

Javasolta: Miklós Szilárd (Herceghalom)

(5 pont)

A beküldési határidő 2012. június 11-én LEJÁRT.

Megoldás. Tegyük fel először, hogy a háromszög szögeire a szokásos jelölésekkel $\alpha$ , $\gamma$ <150^o és $\beta$ <120^o teljesül, vagyis a szóban forgó egyenesek az ábrának megfelelően részben a háromszög belsejében haladnak. Vezessük be még a

$HAC\sph=\alpha_1, BAH\sph=\alpha_2, IBA\sph=\beta_1, CBI\sph=\beta_2, GCB\sph=\gamma_1, ACG\sph=\gamma_2$

jelöléseket.

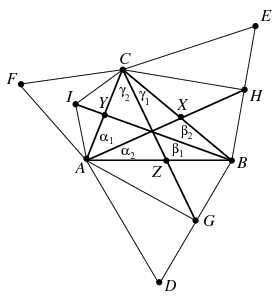
Az ACH, illetve ABH háromszögekre a szinusz-tételt felírva

$\frac{\sin\alpha_1}{\sin(\gamma+30^\circ)}=\frac{CH}{AH},\quad \frac{\sin\alpha_2}{\sin(\beta+60^\circ)}=\frac{BH}{AH},$

ahonnan

$\frac{\sin\alpha_1}{\sin\alpha_2}= \frac{\sin(\gamma+30^\circ)}{\sin(\beta+60^\circ)}\cdot \frac{CH}{BH}= \sqrt{3}\cdot\frac{\sin(\gamma+30^\circ)}{\sin(\beta+60^\circ)}.$

Hasonlóképpen kapjuk, hogy

$\frac{\sin\beta_1}{\sin\beta_2}= \frac{\sin(\alpha+30^\circ)}{\sin(\gamma+30^\circ)}\cdot \frac{AI}{CI}= \frac{\sin(\alpha+30^\circ)}{\sin(\gamma+30^\circ)}$

és

$\frac{\sin\gamma_1}{\sin\gamma_2}= \frac{\sin(\beta+60^\circ)}{\sin(\alpha+30^\circ)}\cdot \frac{BG}{AG}= \frac{1}{\sqrt{3}}\cdot\frac{\sin(\beta+60^\circ)}{\sin(\alpha+30^\circ)}.$

Következésképpen

$\frac{\sin\alpha_1}{\sin\alpha_2}\cdot\frac{\sin\beta_1}{\sin\beta_2}\cdot \frac{\sin\gamma_1}{\sin\gamma_2}=1.$

Most írjuk fel a szinusz-tételt az ACX és ABC háromszögekre, innen a

$\frac{\sin\alpha_1}{\sin\alpha_2}= \frac{\sin\gamma}{\sin\beta}\cdot \frac{XC}{BX}$

összefüggést kapjuk. Hasonlóképpen

$\frac{\sin\beta_1}{\sin\beta_2}= \frac{\sin\alpha}{\sin\gamma}\cdot \frac{YA}{CY}$

és

$\frac{\sin\gamma_1}{\sin\gamma_2}= \frac{\sin\beta}{\sin\alpha}\cdot \frac{ZB}{AZ}.$

Ezeket összeszorozva egyszerűsítés után

$\frac{XC}{BX}\cdot\frac{YA}{CY}\cdot\frac{ZB}{AZ}=1$

adódik, amivel a bizonyítandó állítást visszavezettük Ceva tételére.

Ha $\alpha$ =150^o, $\beta$ =120^o vagy $\gamma$ =150^o, akkor a fenti indoklás során 0-val is kellene osztanunk. Könnyen látható azonban, hogy ekkor a három egyenes rendre az A, B, illetve C csúcsban metszi egymást. Végül ha valamelyik szög túl nagy, akkor a fenti bizonyítás érvényben marad ha irányított szögekkel, illetve szakaszokkal dolgozunk; az $\alpha$ _i, $\beta$ _i, $\gamma$ _i szögek szinuszai közül és az AZ,ZB,BX,XC,CY,YA szakaszok hossza közül is pontosan kettő negatív lesz.

Statisztika:

18 dolgozat érkezett.

5 pontot kapott: Bingler Arnold, Demeter Dániel, Forrás Bence, Herczeg József, Janzer Olivér, Kabos Eszter, Maga Balázs, Mester Márton, Ódor Gergely, Szabó 928 Attila.

4 pontot kapott: Balogh Tamás, Sagmeister Ádám, Zsiros Ádám.

3 pontot kapott: 3 versenyző.

0 pontot kapott: 2 versenyző.

A KöMaL 2012. májusi matematika feladatai

18 dolgozat érkezett.
5 pontot kapott:	Bingler Arnold, Demeter Dániel, Forrás Bence, Herczeg József, Janzer Olivér, Kabos Eszter, Maga Balázs, Mester Márton, Ódor Gergely, Szabó 928 Attila.
4 pontot kapott:	Balogh Tamás, Sagmeister Ádám, Zsiros Ádám.
3 pontot kapott:	3 versenyző.
0 pontot kapott:	2 versenyző.

Már regisztráltál?
Új vendég vagy?