 |
A B. 4659. feladat (2014. október) |
B. 4659. Adott az egységkörlapon \(\displaystyle n\) pont. Legfeljebb mennyi lehet a páronkénti távolságaik szorzata?
(6 pont)
A beküldési határidő 2014. november 10-én LEJÁRT.
1. megoldás. Belátjuk, hogy a távolságok szorzata legfeljebb \(\displaystyle n^{n/2}\), amely értéket \(\displaystyle n=1\)-re mindig felvesz, \(\displaystyle n=2\)-re éppen egymással átellenes pontok esetén vesz fel, \(\displaystyle n\ge 3\)-ra pedig pontosan akkor veszi fel, ha egy, a körbe írt szabályos \(\displaystyle n\)-szög csúcsait jelöltük ki.
Az \(\displaystyle n=1\) esetben nem lép fel távolság, vagyis akár nem értelmezzük a távolságok szorzatát, vagy üres szorzatként tekintünk rá. Utóbbi esetben az eredmény valóban \(\displaystyle 1=1^{1/2}\).
Ha \(\displaystyle n=2\), akkor triviálisan egy átmérő két végpontja adja a maximumális távolságot, az egyetlen fellépő távolság "szorzata" pedig ekkor \(\displaystyle 2=2^{2/2}\).
A továbbiakban feltesszük, hogy \(\displaystyle n\ge 3\).
Legyen \(\displaystyle P_1,P_2,\dots,P_n\) tetszőleges \(\displaystyle n\) darab pont a \(\displaystyle K\) egységkörlapon. Helyezzük el az ábrát a komplex síkon - legyen \(\displaystyle K\) az origó középpontú egységkörlap, és jelölje a \(\displaystyle P_1,P_2\dots,P_{n-1},P_n\) pontokhoz tartozó komplex számokat \(\displaystyle z_1,z_2,\dots,z_{n-1},z_n\). Feltesszük, hogy páronként különböző pontokról van szó, egyébként a távolságszorzat nulla és triviális a kérdés.
Első lépésben belátjuk, hogy ha valamely \(\displaystyle P_i\) pont, mondjuk \(\displaystyle P_n\) az egységkör belsejébe esik, akkor kicserélhető olyan pontra az egységkörvonalon, amelyre már nagyobb a távolságok páronként vett szorzata. Vagyis sorban lecserélhetjük minden, a kör belsejében lévő pontot egy kerületi pontra, a szorzatot eközben növelve. Tehát ebből következik, hogy elég megkeresni a maximumot abban az esetben, hogy minden \(\displaystyle P_i\) pont \(\displaystyle K\) kerületén található.
Feltettük, hogy \(\displaystyle P_n\) esik \(\displaystyle K\) belsejébe. Vizsgáljuk meg, hogyan függ \(\displaystyle P_n\) elhelyezkedésétől, azaz \(\displaystyle z_n\) komplex számtól a \(\displaystyle P_i\)-k közötti távolságok páronként vett szorzata! A távolságszorzat
\(\displaystyle f(z_n)=\prod_{1\le i<j\le n}P_iP_j=\prod_{1\le i<j\le n}|z_i-z_j|=\left|\left(\prod_{1\le i<j\le n-1}(z_i-z_j)\right)\cdot (z_n-z_1)(z_n-z_2)\dots(z_n-z_{n-1})\right|,\)
vagyis \(\displaystyle f(z)\) egy \(\displaystyle (n-1)\)-edfokú komplex együtthatós polinom abszolútértéke (a zárójelben nem nulla tényező áll, hisz a pontok különbözőek).
Ismert a holomorf függvények maximum-elve, amely szerint bármely egyszeresen összefüggő nyílt tartományon értelmezett nemkonstans holomorf függvény abszolút értékének csak a tartomány szélén lehet lokális maximuma. (Lásd pl. a következő weblapokon:
http://hu.wikipedia.org/wiki/Holomorf_függvények,
http://mathworld.wolfram.com/MaximumModulusPrinciple.html,
http://en.wikipedia.org/wiki/Maximum_modulus_principle.)
Az \(\displaystyle f(z)\) egy, a \(\displaystyle K\) körlapon értelmezett \(\displaystyle (n-1)\)-edfokú polinom. Itt \(\displaystyle K\) körlap belseje egy egyszeresen összefüggő nyílt tartomány, \(\displaystyle f\) pedig polinom lévén mindenhol deriválható (http://hu.wikipedia.org/wiki/Holomorf_függvények), vagyis holomorf. Mivel \(\displaystyle f\) nem konstans, ezért a maximum-elvet alkalmazva, kapjuk, \(\displaystyle K\) belsején nem lehet lokális maximuma.
Azt is tudjuk, hogy \(\displaystyle f\) egy kompakt halmazon értelmezett, valós értékű folytonos függvény (hisz két folytonos függvény szorzata folytonos, és a távolságmérték-függvény folytonos). Weierstrass tétele szerint ezért \(\displaystyle f\) valamely \(\displaystyle z^*\) helyen maximális. Eme abszolút maximum persze egyben lokális maximum, ezért a maximum-elv szerint \(\displaystyle z^*\) csak \(\displaystyle K\) kerületén lehet. Mivel pedig \(\displaystyle z^*\) maximum, ám \(\displaystyle z_n\) belső pont lévén nem lehet az, így \(\displaystyle f(z_n)<f(z^*)\).
Ezzel beláttuk első állításunkat, és elegendő a távolságszorzat maximumát a \(\displaystyle K\) kerületén lévő pont-\(\displaystyle n\)-esekre vizsgálni. (Továbbá a maximális szorzat csak kerületi pontoknál léphet fel.)
Tegyük fel, hogy \(\displaystyle P_1,P_2,\dots,P_n\) pontok az \(\displaystyle O\) középpontú egységkör kerületén vannak, és az általánosság megszorítása nélkül tegyük fel, hogy pozitív körüljárás szerint ebben a sorrendben szerepelnek (ilyenkor tehát \(\displaystyle P_1P_2\dots P_n\) konvex sokszög). Feltehetjük, hogy bármely két \(\displaystyle P_i\) különböző. Kényelmi okokból indexeljünk modulo \(\displaystyle n\), legyen \(\displaystyle P_{i+n}=P_i\) bármely \(\displaystyle i\)-re.
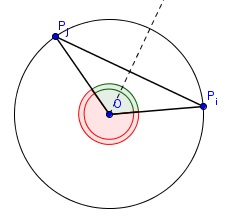
1. ábra
Tekintsük a \(\displaystyle P_iOP_j\) egyenlő szárú háromszöget. Húzzuk be a háromszög szimmetriatengelyét, ez két olyan derékszögű háromszögre bontja, melynek \(\displaystyle O\)-nál lévő szöge \(\displaystyle \frac{P_iOP_j\angle}2\), és átfogója \(\displaystyle OP_i=OP_j=1\). Jelölje \(\displaystyle \theta_{i,j}\in(0;2\pi)\) azt a forgásszöget, amivel \(\displaystyle OP_i\) az \(\displaystyle OP_j\) szakaszba forgatható, ekkor \(\displaystyle \theta_{i,j}=P_iOP_j\angle\) vagy \(\displaystyle \theta_{i,j}=2\pi-P_iOP_j\angle\). Mivel viszont \(\displaystyle \sin x=\sin(\pi-x)\), ezért kapjuk:
\(\displaystyle P_iP_j=2\sin\frac{P_iOP_j\angle}2=2\sin\frac{\theta_{i,j}}2.\)
Ebből következik, hogy minden \(\displaystyle 1\le k\le n-1\) esetén
\(\displaystyle \prod_{i=1}^nP_iP_{i+k}=2^n\prod_{i=1}^n \sin\frac{\theta_{i,i+k}}2,\)
és mivel a tényezők pozitívak, így logaritmust is vehetünk:
| \(\displaystyle \log\prod_{i=1}^n P_iP_{i+k}=\log 2^n+\sum_{i=1}^n\log\sin\frac{\theta_{i,i+k}}2.\) | \(\displaystyle (1)\) |
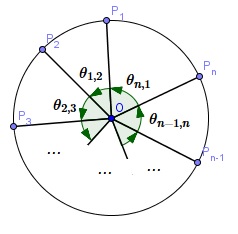
2. ábra
Mivel \(\displaystyle P_1,P_2,\dots,P_n\) pozitív körüljárás szerint szerepel, ezért \(\displaystyle \theta_{i,i+1}\) jelöli az egységkörön a \(\displaystyle P_i\)-től \(\displaystyle P_{i+1}\)-ig tartó ívhosszt, vagyis \(\displaystyle \sum_{i=1}^n\theta_{i,i+1}\) összeg éppen az egységkör kerületével, \(\displaystyle 2\pi\)-vel azonos. Innen kapjuk, hogy bármely \(\displaystyle 1\le k\le n-1\)-re
| \(\displaystyle \sum_{i=1}^n\theta_{i,i+k}=\sum_{i=1}^n(\theta_{i,i+1}+\theta_{i+1,i+2}+\dots+\theta_{i+k-1,i+k})=k\cdot \sum_{i=1}^n\theta_{i,i+1}=2\pi k.\) | \(\displaystyle (2)\) |
Mi több, \(\displaystyle t\in(0;2\pi)\) esetén a \(\displaystyle g(t)=\log\sin\frac t2\) függvény deriváltja a láncszabályt felhasználva:
\(\displaystyle g'(t)=\frac1{\sin\frac t2}\cdot \cos\frac t2\cdot \frac12=\frac12\ctg\frac t2,\)
és ennek deriváltja ismert módon
\(\displaystyle g''(t)=-\frac14\frac1{\cos^2\frac t2}<0.\)
Ebből következik, hogy \(\displaystyle g(t)\) a \(\displaystyle (0;2\pi)\) intervallumon szigorúan konkáv. A Jensen-egyenlőtlenséget ezért alkalmazhatjuk a \(\displaystyle \theta_{i,i+k}\in(0;2\pi)\) számokra:
| \(\displaystyle \frac1n\sum_{i=1}^n g(\theta_{i,i+k})\le g\left(\frac1n\sum_{i=1}^n \theta_{i,i+k}\right).\) | \(\displaystyle (3)\) |
Ebbe beírva \(\displaystyle (2)\)-t:
\(\displaystyle \sum_{i=1}^n \log\sin\frac{\theta_{i,i+k}}2\le n\cdot g\left(\frac{2\pi k}n\right)=n\cdot \log\sin \frac{k\pi}n,\)
vagyis \(\displaystyle (1)\)-ben
\(\displaystyle \log\prod_{i=1}^n P_iP_{i+k}=\log 2^n+\sum_{i=1}^n\log\sin\frac{\theta_{i,i+k}}2\le \log 2^n+n\cdot \log\sin\frac{k\pi}n=\log\left(2\sin\frac{k\pi}n\right)^n,\)
és az exponenciális függvény szigorú monoton növekvőségét felhasználva
\(\displaystyle \prod_{i=1}^n P_iP_{i+k}\le \left(2\sin\frac{k\pi}n\right)^n\qquad \forall k=1,2,\dots,n-1.\)
Ezt összeszorozva \(\displaystyle k=1,2,\dots,n-1\)-re:
| \(\displaystyle \prod_{k=1}^{n-1}\left(2\sin\frac{k\pi}n\right)^n\ge \prod_{k=1}^{n-1}\prod_{i=1}^n P_iP_{i+k}=\prod_{i=1}^n\prod_{k=1}^{n-1}P_iP_{i+k}=\prod_{i=1}^n \prod_{j\neq i}P_iP_j=\left(\prod_{1\le i<j\le n}P_iP_j\right)^2.\) | \(\displaystyle (4)\) |
Legyen most \(\displaystyle \epsilon=\cos\frac\pi n+i\sin\frac{\pi}n\), akkor a De Moivre-képlet szerint \(\displaystyle \epsilon^k=\cos\frac{k\pi}n+i\sin\frac{k\pi}n\), amiért
\(\displaystyle \frac{\epsilon^k-\overline{\epsilon^k}}i=\frac{\left(\cos\frac{k\pi}n+i\sin\frac{k\pi}n\right)-\left(\cos\frac{k\pi}n-i\sin\frac{k\pi}n\right)}i=2\sin\frac{k\pi}n.\)
Továbbá a konjugálás azonosságaiból \(\displaystyle \overline{\epsilon^k}=\overline{\epsilon}^k=\epsilon^{-k}\). Mivel pozitív valós szám, ezért adódik, hogy
\(\displaystyle \prod_{k=1}^{n-1}2\sin\frac{k\pi}n=\left|\prod_{k=1}^{n-1}2\sin\frac{k\pi}n\right|=\)
\(\displaystyle =\left|\prod_{k=1}^n \frac{\epsilon^k-\epsilon^{-k}}i\right|=\left|\prod_{k=1}^{n-1}(1-\epsilon^{2k})\right|,\)
ahol az utolsó átalakításnál minden tényezőt egy egységnyi abszolút értékű komplex számmal szoroztunk. Mivel \(\displaystyle \epsilon^2,\epsilon^4,\dots,\epsilon^{2n-2}\) éppen a komplex \(\displaystyle n\)-edik egységgyökök a De Moivre-képlet szerint, ezért gyöktényezőik az \(\displaystyle \frac{x^n-1}{x-1}=x^{n-1}+\dots+1\) polinomnak. Ezt \(\displaystyle x=1\)-re használva:
\(\displaystyle \prod_{k=1}^{n-1}(1-\epsilon^{2k})=1^{n-1}+1^{n-2}+\dots+1=n.\)
A kapott eredményt beírva \(\displaystyle (4)\)-be:
\(\displaystyle \prod_{1\le i<j\le n}P_iP_j\le n^{n/2}.\)
Ebben a becslésben egyenlőség is fennállhat, pontosan akkor, hogyha \(\displaystyle (3)\)-ban mindig egyenlőség van, azaz ha \(\displaystyle \theta_{1,1+k}=\theta_{2,2+k}=\dots=\theta_{n,n+k}\) mindegyik \(\displaystyle k=1,2,\dots,n-1\)-re. Mindez éppen akkor érhető el, hogyha \(\displaystyle P_1P_2\dots P_n\) egy szabályos \(\displaystyle n\)-szög.
Tehát a páronként vett távolságok szorzata legfeljebb \(\displaystyle n^{n/2}\).
Williams Kada Szegedi Radnóti M. Kísérleti Gimn., 10. o. t
2. megoldás. A pontokat ismét vegyük fel a komplex egységkörben: \(\displaystyle z_1,\dots,z_n\). A pontokból készített Vandermonde-determinánsra írjuk fel a Hadamard-egyenlőtlenséget :
\(\displaystyle \left|\prod_{1\le j<k\le n} (z_k-z_j)\right| = \left| {\rm det} \left(\matrix{ 1 & z_1 & z_1^2 & \dots & z_1^{n-1} \cr 1 & z_2 & z_2^2 & \dots & z_2^{n-1} \cr \dots & \dots & \dots & & \dots \cr 1 & z_n & z_n^2 & \dots & z_n^{n-1} \cr}\right) \right| \le \prod_{j=1}^n \sqrt{1^2+|z_j|^2+|z_j|^4+\dots+|z_j|^{2n-2}} \le (\sqrt{n})^n. \)
Ha a pontok az egységkörbe írt szabályos \(\displaystyle n\)-szög csúcsai, akkor egyenlőség áll. Ez leolvasható a megoldásból, de közvetlenül is ellenőrizhető.
Statisztika:
12 dolgozat érkezett. 6 pontot kapott: Fekete Panna, Williams Kada. 5 pontot kapott: Kovács 972 Márton. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 4 versenyző. 0 pontot kapott: 4 versenyző.
A KöMaL 2014. októberi matematika feladatai

