A B. 5069. feladat (2019. december)

B. 5069. Az \(\displaystyle ABCD\) deltoid szimmetriatengelye \(\displaystyle AC\). Az \(\displaystyle AB\) oldalra \(\displaystyle B\)-ben, és a \(\displaystyle CD\) oldalra \(\displaystyle D\)-ben állított merőlegesek metszéspontja \(\displaystyle M\). Mutassuk meg, hogy \(\displaystyle AMD\sphericalangle=BMC\sphericalangle\).

(6 pont)

A beküldési határidő 2020. január 10-én LEJÁRT.

Megoldás. Legyen az \(\displaystyle M\) pont merőleges vetülete az \(\displaystyle AC\) egyenesen \(\displaystyle T\). Mivel \(\displaystyle ABM\measuredangle=MTA\measuredangle=MTC\measuredangle=MDC\measuredangle=90^\circ\), a Thalész-tétel megfordítása szerint az \(\displaystyle A,B,M,T\), illetve a \(\displaystyle C,D,M,T\) pontok egy körön vannak. Emiatt (irányított, modulo \(\displaystyle 180^\circ\) szögekkel számolva) \(\displaystyle BMA\measuredangle=BTA\measuredangle\), illetve \(\displaystyle CMD\measuredangle=CTD\measuredangle\). Mivel \(\displaystyle T\) a deltoid szimmetriatengelyén van, a \(\displaystyle BTA\measuredangle=BTC\measuredangle\) és \(\displaystyle ATD\measuredangle=CTD\measuredangle\) szögek egymás tükörképei. Tehát

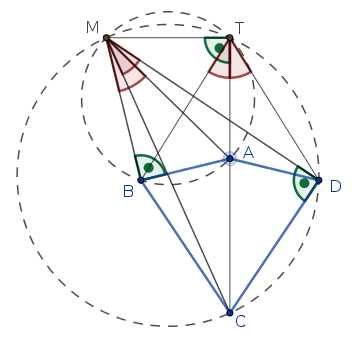
A \(\displaystyle (*)\) egyenletet egyelőre csak irányított szögekkel tudjuk, tehát \(\displaystyle CMD\measuredangle\) és \(\displaystyle BMA\measuredangle\) vagy azonos irányítású, és akkor egyenlők, vagy pedig ellentétes irányításúak, és akkor az összegük \(\displaystyle 180^\circ\). De vegyük észre, hogy ez a két szög a derékszögű \(\displaystyle CDM\) és \(\displaystyle BMA\) háromszögek hegyesszögei, az összegük biztosan kisebb \(\displaystyle 180^\circ\)-nál. Tehát, \(\displaystyle CMD\measuredangle\) és \(\displaystyle BMA\measuredangle\) csak azonos irányítású, egyenlő nagyságú hegyesszögek lehetnek.

Végül tekintsük azt az \(\displaystyle M\) körüli, \(\displaystyle BMA\measuredangle=CMD\measuredangle\) szögű forgatást, amely az \(\displaystyle MB\) félegyenest az \(\displaystyle MA\) félegyenesbe, az \(\displaystyle MC\) félegyenest pedig az \(\displaystyle MD\) félegyenesbe viszi. Ez a forgatás a \(\displaystyle BMC\measuredangle\) szöget az \(\displaystyle AMD\measuredangle\) szögbe viszi, tehát a két szög egyenlő: \(\displaystyle BMC\measuredangle=AMD\measuredangle\), és éppen ezt kellett igazolnunk.

Statisztika:

42 dolgozat érkezett.
6 pontot kapott:	Andó Viola, Argay Zsolt, Bán-Szabó Áron, Baski Bence, Beke Csongor, Bencsik Ádám, Bursics András, Csonka Illés, Fekete Richárd, Fleiner Zsigmond, Füredi Erik Benjámin, Geretovszky Anna, Gyetvai Miklós, Hámori Janka, Hegedűs Dániel, Hervay Bence, Jánosik Áron, Kercsó-Molnár Anita, Kerekes Boldizsár, Kitschner Bernadett, Kocsis Anett, Kovács 129 Tamás, Lazur Zsófia, Lengyel Ádám, Lovas Márton, Mátravölgyi Bence, Molnár-Szabó Vilmos, Nádor Benedek, Nagy 551 Levente, Németh Márton, Nguyen Bich Diep, Osztényi József, Seres-Szabó Márton, Somogyi Dalma, Szabó 991 Kornél, Sztranyák Gabriella, Tiderenczl Dániel, Velich Nóra.
5 pontot kapott:	Molnár Lehel.
3 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2019. decemberi matematika feladatai