A B. 5075. feladat (2020. január)

B. 5075. Az $\displaystyle ABCD$ konvex négyszög $\displaystyle AD$ és $\displaystyle BC$ oldalainak felezőpontja $\displaystyle E$, illetve $\displaystyle F$. Az $\displaystyle EF$ szakasz az $\displaystyle AC$ átlót a $\displaystyle P$ pontban, a $\displaystyle BD$ átlót $\displaystyle Q$-ban metszi. Bizonyítsuk be, hogy az $\displaystyle AEP$ és $\displaystyle BFQ$ körök az $\displaystyle AB$ egyenesen metszik egymást.

Javasolta: Holló Gábor (Budapest)

(5 pont)

A beküldési határidő 2020. február 10-én LEJÁRT.

Megoldás. Legyen $\displaystyle AB$ felezőpontja $\displaystyle G$, és legyen $\displaystyle X$ az $\displaystyle EFG$ kör második, $\displaystyle G$-től különböző metszéspontja az $\displaystyle AGB$ egyenessel; ha az $\displaystyle AB$ egyenes $\displaystyle G$-ben érinti az $\displaystyle EFG$ kört, akkor legyen $\displaystyle X=G$. Azt fogjuk igazolni, hogy az $\displaystyle AEP$ és a $\displaystyle BFQ$ kör is átmegy az $\displaystyle X$ ponton. Mivel az $\displaystyle A$ és $\displaystyle B$ pontok szerepe felcserélhető, elég azt igazolnunk, hogy az $\displaystyle AEP$ kör átmegy $\displaystyle X$-en.

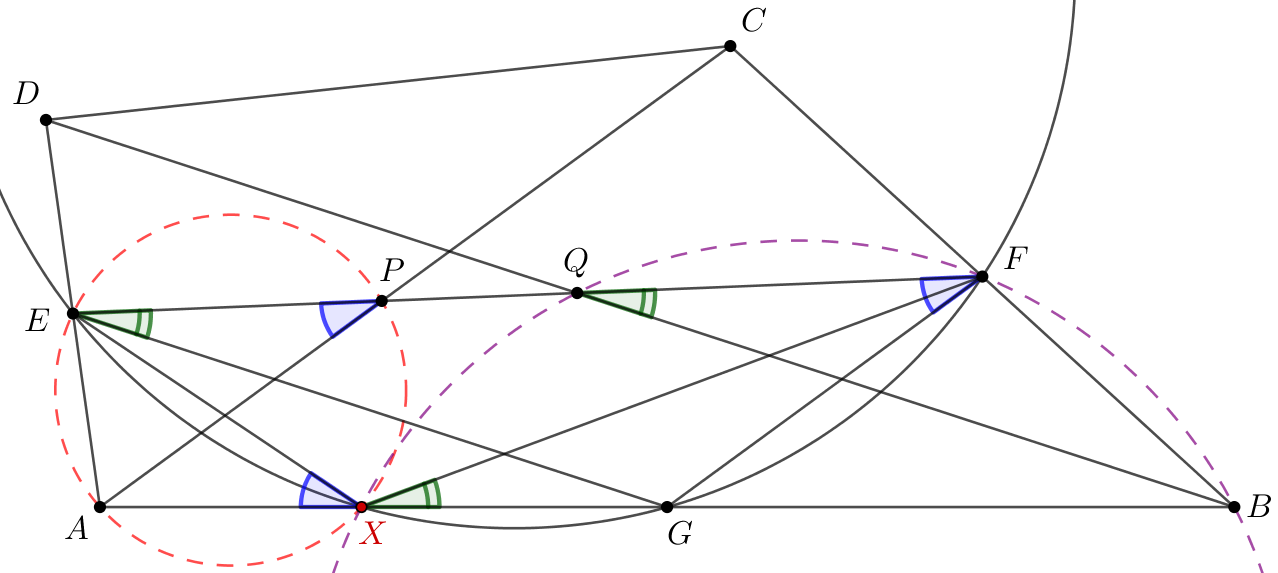
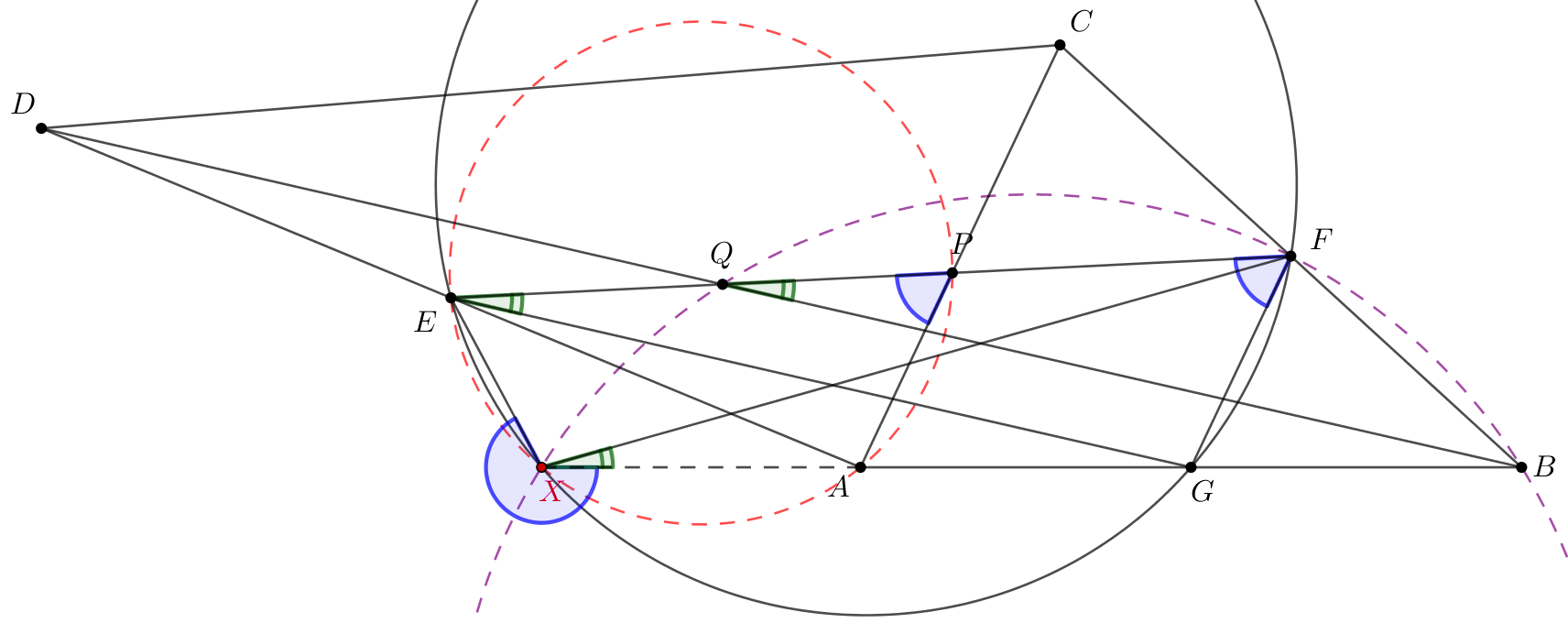
Az $\displaystyle X$ pont az $\displaystyle AB$ szakaszon kívülre is eshet. Azért, hogy lerövidítsük a különféle esetek diszkusszióját, irányított (modulo $\displaystyle 180^\circ$) szögekkel fogunk számolni: $\displaystyle \measuredangle(e,f)$ azt a szöget jelenti, amellyel az $\displaystyle e$ egyenest pozitív irányban az $\displaystyle f$ egyenesbe lehet forgatni.

Ha $\displaystyle X$ egybeesik az $\displaystyle A$ ponttal, akkor persze $\displaystyle X$ az $\displaystyle AEP$ körön van, és nincs mit bizonyítanunk. A továbbiakban feltételezzük, hogy $\displaystyle X\ne A$.

Ha az $\displaystyle AB$ egyenes metszi az $\displaystyle EFG$ kört, akkor $\displaystyle X\ne G$, és az $\displaystyle EFGX$ körben $\displaystyle \measuredangle(EX,AX)=\measuredangle(EX,GX)=\measuredangle(EF,GF)$. Ha az $\displaystyle AB$ egyenes $\displaystyle G$-ben érinti az $\displaystyle EFG$ kört, akkor $\displaystyle X$ egybeesik a $\displaystyle G$ ponttal, és $\displaystyle \measuredangle(EX,AX)$ a körnek az $\displaystyle EG$ húrhoz tartozó érintő szárú kerületi szöge, tehát ilyenkor is $\displaystyle \measuredangle(EX,AX)=\measuredangle(EF,GF)$.

A $\displaystyle GF$ szakasz az $\displaystyle ABC$ háromszögben az $\displaystyle AC$-vel párhuzamos középvonal, így $\displaystyle \measuredangle(EF,GF)=\measuredangle(EF,AC)=\measuredangle(EP,AP)$. Tehát $\displaystyle \measuredangle(EX,AX)=\measuredangle(EF,GF)=\measuredangle(EP,AP)$, és emiatt $\displaystyle A,E,P,X$ egy körön van. Ezzel az állítást igazoltuk.

Statisztika:

17 dolgozat érkezett.
5 pontot kapott:	Al-Hag Máté Amin, Andó Viola, Bán-Szabó Áron, Baski Bence, Beke Csongor, Csonka Illés, Fleiner Zsigmond, Geretovszky Anna, Hámori Janka, Hegedűs Dániel, Jánosik Áron, Kovács 129 Tamás, Nagy 551 Levente, Nguyen Bich Diep, Sztranyák Gabriella, Tiderenczl Dániel, Velich Nóra.

A KöMaL 2020. januári matematika feladatai