 |
A B. 5180. feladat (2021. május) |
B. 5180. Az \(\displaystyle ABCDEFG\) szabályos hétszög köré írt kör sugara \(\displaystyle r\). Igazoljuk, hogy az \(\displaystyle A\) középpontú, \(\displaystyle 2r\) sugarú kör átmegy a \(\displaystyle BCE\) háromszög magasságpontján.
(5 pont)
A beküldési határidő 2021. június 10-én LEJÁRT.
Megoldás. Legyen a hétszög középpontja \(\displaystyle O\), a \(\displaystyle BCE\) háromszög magasságpontja \(\displaystyle M\). Azt kell igazolnunk, hogy \(\displaystyle AM=2r\).
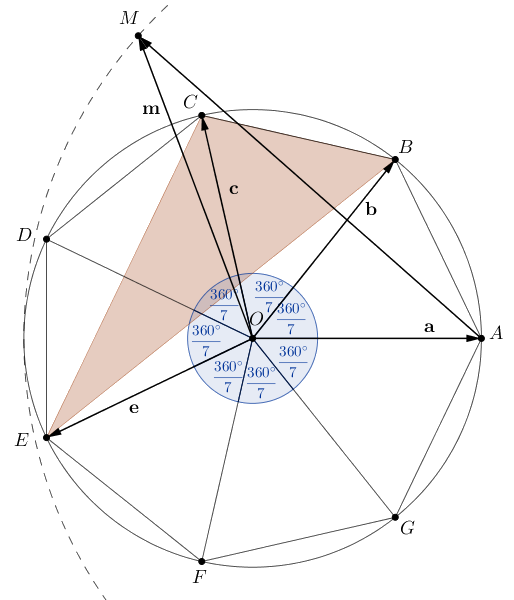
Legyen
\(\displaystyle \mathbf{a}=\overrightarrow{OA}, \quad \mathbf{b}=\overrightarrow{OB}, \quad \mathbf{c}=\overrightarrow{OC}, \quad \mathbf{e}=\overrightarrow{OE} \quad \text{és} \quad \mathbf{m}=\overrightarrow{OM}. \)
A hétszög köré írt kör középontja \(\displaystyle O\), ezért
\(\displaystyle |\mathbf{a}|=|\mathbf{b}|=|\mathbf{c}|=|\mathbf{e}|=r. \)
Az \(\displaystyle O\) pont egyben a \(\displaystyle BCE\) háromszög köré írt kör középontja is, ezért
\(\displaystyle \mathbf{m} = \overrightarrow{OM} = \overrightarrow{OB} +\overrightarrow{OC} +\overrightarrow{OE} = \mathbf{b}+\mathbf{c}+\mathbf{e}, \)
tehát
\(\displaystyle \overrightarrow{AM} = \overrightarrow{OM}-\overrightarrow{OA} = (\mathbf{b}+\mathbf{c}+\mathbf{e}) -\mathbf{a}. \)
Emeljük négyzetre skalárisan az \(\displaystyle \overrightarrow{AM}\) vektort:
$$\begin{align*} AM^2 &= \Big(\overrightarrow{AM}\Big)^2 = (\mathbf{b}+\mathbf{c}+\mathbf{e}-\mathbf{a})^2 = \mathbf{b}^2+\mathbf{c}^2+\mathbf{e}^2+\mathbf{a}^2 +2\mathbf{b}\mathbf{c} +2\mathbf{b}\mathbf{e} +2\mathbf{c}\mathbf{e} -2\mathbf{a}\mathbf{b} -2\mathbf{a}\mathbf{c} -2\mathbf{a}\mathbf{e}= \\ &= 4r^2 +2(\mathbf{b}\mathbf{c}-\mathbf{a}\mathbf{b}) +2(\mathbf{c}\mathbf{e}-\mathbf{a}\mathbf{c}) +2(\mathbf{b}\mathbf{e}-\mathbf{a}\mathbf{e}). \tag{*} \end{align*}$$Vegyük észre, hogy \(\displaystyle AOB\sphericalangle=BOC\sphericalangle=\frac{360^\circ}{7}\) miatt \(\displaystyle \mathbf{a}\mathbf{b}=\mathbf{b}\mathbf{c}\), \(\displaystyle AOC\sphericalangle=COE\sphericalangle=\frac{2\cdot360^\circ}{7}\) miatt \(\displaystyle \mathbf{a}\mathbf{c}=\mathbf{c}\mathbf{e}\), és ugyanígy \(\displaystyle EOA\sphericalangle=BOE\sphericalangle=\frac{3\cdot360^\circ}{7}\) miatt \(\displaystyle \mathbf{a}\mathbf{e}=\mathbf{b}\mathbf{e}\). A \(\displaystyle (*)\) jobboldalán ezek a tagok mind kiesnek, ezzel azt kapjuk, hogy
\(\displaystyle AM^2 = 4r^2, \)
vagyis
\(\displaystyle AM = 2r, \)
és éppen ezt kellett igazolni.
Statisztika:
33 dolgozat érkezett. 5 pontot kapott: Arató Zita, Bán-Szabó Áron, Baski Bence, Csonka Illés, Diaconescu Tashi, Dienes Ervin Fotisz, Fekete Richárd, Hegedűs Dániel, Kalocsai Zoltán, Kercsó-Molnár Anita, Koleszár Domonkos, Lovas Márton, Mohay Lili Veronika, Móricz Benjámin, Nádor Benedek, Nagy 551 Levente, Németh Márton, Osztényi József, Romaniuc Albert-Iulian, Seres-Szabó Márton, Simon László Bence, Somogyi Dalma, Sztranyák Gabriella, Török Ágoston, Wiener Anna, Zömbik Barnabás. 4 pontot kapott: Beinschroth Ninett, Csizmadia Miklós, Molnár-Szabó Vilmos. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző.
A KöMaL 2021. májusi matematika feladatai
