 |
A B. 5403. feladat (2024. szeptember) |
B. 5403. Tegyük fel, hogy egy egyszerű, összefüggő \(\displaystyle k\)-reguláris (\(\displaystyle k \ge 2\)) \(\displaystyle G\) gráf éleit ki lehet színezni \(\displaystyle k\) színnel úgy, hogy minden csúcsban csupa különböző színű él találkozzon. Bizonyítsuk be, hogy \(\displaystyle G\) bármelyik élét törölve a kapott gráf is összefüggő.
Javasolta: Hujter Bálint, Budapest
(5 pont)
A beküldési határidő 2024. október 10-én LEJÁRT.
Előzetes megoldás. Színezzük ki a gráf éleit \(\displaystyle k\) színnel úgy, hogy minden csúcsban csupa különböző színű él találkozzon. Ilyenkor, ha egyet kiválasztunk a \(\displaystyle k\) szín közül, és csak az ilyen színű éleket tekintjük, akkor észrevehetjük, hogy minden csúcsba pont egy ilyen színű él fut be, ezek az élek tehát teljes párosítást alkotnak. (Mellékes következmény, hogy a gráf csúcsszáma biztosan páros).
Indirekt tegyük fel, hogy az \(\displaystyle e\) él törlésével szétesik a gráf, azaz a keletkező \(\displaystyle G'\) gráf már nem összefüggő.
\(\displaystyle G'\) tehát nem összefüggő, de kettőnél több komponense sem lehet, hiszen az \(\displaystyle e\) él csak kettőt tud összekötni a komponensek közül (és \(\displaystyle e\) visszatevésével összefüggővé kellene válnia a gráfnak).
Legyen az \(\displaystyle e\) él színe piros, egy másik szín a \(\displaystyle k\) közül pedig kék. A fentiek szerint a törlés előtt a piros élek teljes párosítást alkottak, tehát \(\displaystyle G'\)-ben is igaz, hogy a piros élek az \(\displaystyle e\) él két végén kívül a többi csúcsot bepárosítják. A pároknak egyazon komponensben kell lenniük, míg az \(\displaystyle e\) véginek különböző komponensben. Tehát a két komponens külön-külön páratlan sok csúccsal rendelkezik.
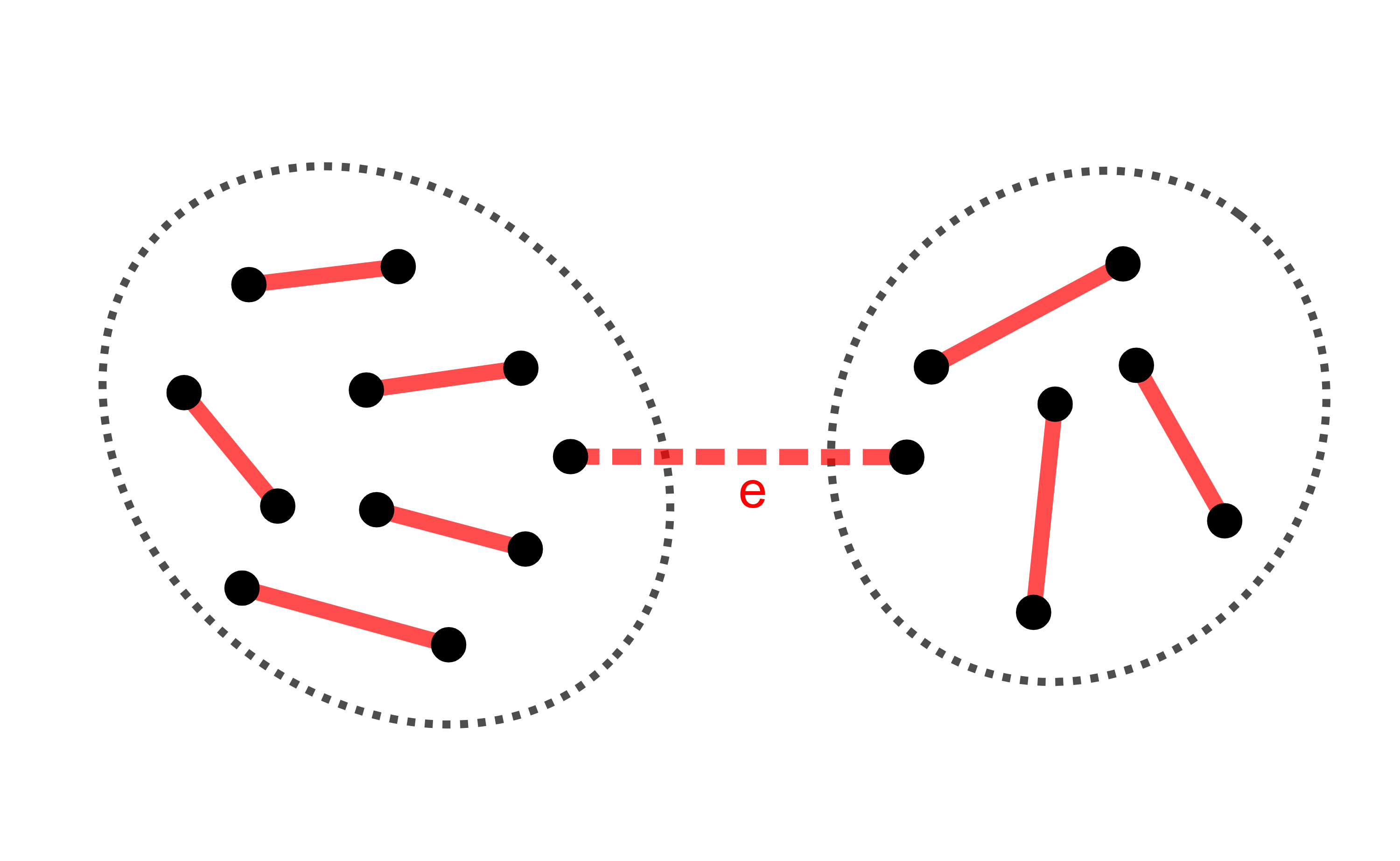
A kék élek ugyanakkor \(\displaystyle G'\)-ben is teljes párosítást alkotnak. Mivel a kék szín szerinti pároknak is egyazon komponensben kell lenniük, ezért minden komponens páros elemszámú kell legyen. Ellentmondás.
Tehát bármelyik élét is töröljük, \(\displaystyle G\) összefüggő marad.
(Ezt úgy is szokás mondani, hogy \(\displaystyle G\) kétszeresen él-összefüggő. Nem tévesztendő össze a kétszeresen összefüggő – avagy kétszeresen csúcs-összefüggő – gráfok fogalmával, amelyek tetszőleges csúcs törlése után is összefüggők maradnak. Minden kétszeresen összefüggő gráf kétszeresen él-összefüggő is, de fordítva már nem igaz.)
1. megoldás. Indirekten bizonyítunk. Tegyük fel, hogy a \(\displaystyle v_1\) és \(\displaystyle v_2\) csúcsokat összekötő él törlése után \(\displaystyle G\) szétesik, azaz \(\displaystyle v_1\) és \(\displaystyle v_2\) különböző összefüggőségi komponensbe kerül. Jelölje \(\displaystyle n\) a \(\displaystyle v_1\) csúcs komponensének csúcsszámát.
Tekintsük \(\displaystyle G\)-nek egy a feltételek szerinti \(\displaystyle k\)-színű élszínezését, amelyben a törölt él színe piros, egy másik szín pedig kék. A \(\displaystyle v_1\) csúcs komponensében az összes csúcsból pontosan 1 kék él indul, tehát a komponensen belüli kék élek száma \(\displaystyle n/2\). Piros él azonban csak \(\displaystyle n-1\) csúcsból indul ki, tehát a komponensen belüli piros élek száma \(\displaystyle (n-1)/2\). Mivel \(\displaystyle n/2\) és \(\displaystyle (n-1)/2\) nem lehet egyszerre egész, ellentmondáshoz jutottunk.
Erdélyi Berta (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 10. o. t.) megoldása alapján
2. megoldás. Vegyünk egy tetszőleges \(\displaystyle e\) élt, és tekintsük \(\displaystyle G\)-nek egy a feladat feltételei szerinti \(\displaystyle k\)-színű élszínezését, amelyben \(\displaystyle e\) színe piros, egy másik szín pedig kék. Ha \(\displaystyle G\)-ből elhagyjuk az összes többi színű élt, egy 2-reguláris gráfot kapunk. A 2-reguláris gráfok diszjunkt körökre bomlanak, \(\displaystyle e\) az egyik körben van, tehát az általa összekötött két csúcsot egy másik úton is el lehet érni egymásból, így \(\displaystyle e\) törlésével nem eshet szét a gráf.
Juhász-Molnár Mirkó (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 10. o. t.) megoldása alapján
3. megoldás. Vegyünk egy tetszőleges \(\displaystyle e\) élt, és tekintsük \(\displaystyle G\)-nek egy a feladat feltételei szerinti \(\displaystyle k\)-színű élszínezését, amelyben \(\displaystyle e\) színe piros, egy másik szín pedig kék. \(\displaystyle G\)-ben tehát minden csúcsából egy piros és egy kék él indul. Tekintsük az \(\displaystyle e\) egyik végpontjából kiinduló kék élt. Ennek a kék élnek a másik végpontjából kiindul egy piros él, annak másik végpontjából egy kék él, és így tovább, egy kék-piros alternáló utat építünk. Ez az alternáló út sehol máshol nem érhet véget, mint \(\displaystyle e\) másik végpontjában. Tehát az \(\displaystyle e\) által összekötött két csúcsot egy másik úton is el lehet érni egymásból, azaz \(\displaystyle e\) törlésével nem eshet szét a gráf.
Pletikoszity Martin (Szegedi Radnóti M. Kís. Gimn., 11. o. t.) megoldása alapján
Megjegyzések. 1. A beérkezett helyes megoldások döntő többsége az 1. megoldáshoz hasonló indirekt bizonyítás: az egy él törlésével keletkezett komponensek paritására hivatkozva jut ellentmondásra (a komal.hu-n is egy ilyen megoldást közöltünk). Mint a másik két megoldásból kiderül, nem szükségszerű a páros-páratlan gondolat a megoldáshoz. A 2. és 3. megoldás nagyon közeli rokonok, mégis közöljük mindkét bizonyítást, a köztük lévő érdekes kapcsolat miatt. Utóbbi indoklás az előbbiben kulcsszerepet játszó közismert állítás (2-reguláris gráfok diszjunkt körökre bomlanak) szokásos bizonyítására rímel.
2. A feladat szorosan kapcsolódik a négyszín-tételhez, illetve néhány egyéb, a 3-reguláris gráfokra vonatkozó érdekes állításhoz, ezekről Hujter Bálint Tait tétele és a 3-reguláris gráfok – a B. 5403. feladat háttere c. cikkében lehet olvasni.
Statisztika:
72 dolgozat érkezett. 5 pontot kapott: 52 versenyző. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 7 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2024. szeptemberi matematika feladatai

