 |
A B. 5495. feladat (2025. december) |
B. 5495. Egy derékszögű háromszög befogói \(\displaystyle a\) és \(\displaystyle b\), átfogója \(\displaystyle c\), beírt körének sugara \(\displaystyle r\). Mutassuk meg, hogy
\(\displaystyle 2r^2=(c-a)(c-b). \)
Javasolta: Kiss Géza (Csömör)
(3 pont)
A beküldési határidő 2026. január 12-én LEJÁRT.
Megoldás. Jelölje a beírt kör középpontját \(\displaystyle I\), az érintési pontjait az \(\displaystyle a\) és \(\displaystyle b\) befogón \(\displaystyle A_1\) és \(\displaystyle B_1\).
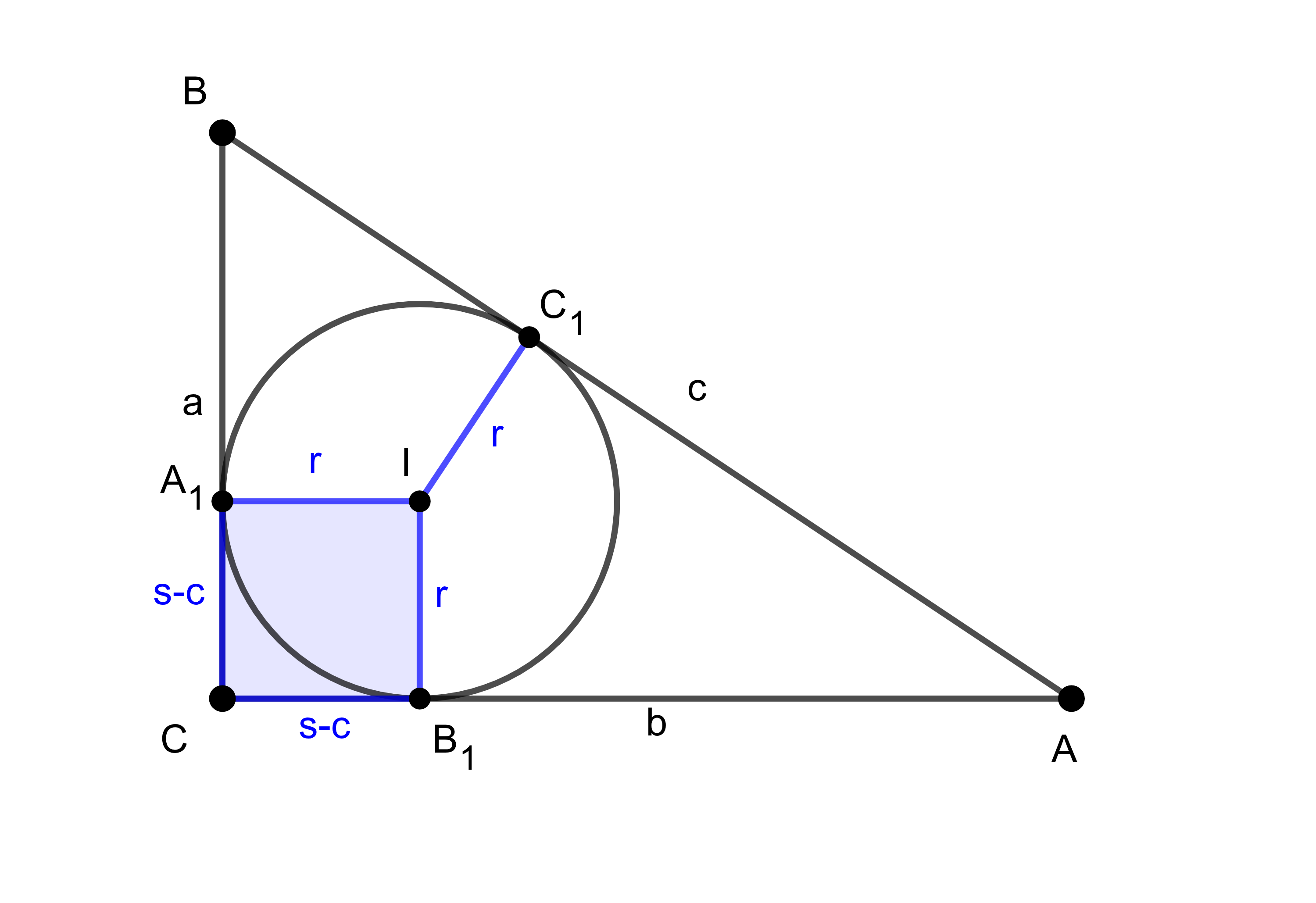
Ismert, hogy tetszőleges háromszögben teljesül, hogy a \(\displaystyle C\) csúcsból a beírt körhöz húzott érintőszakaszok hossza \(\displaystyle s-c\) (ahol \(\displaystyle s\) a félkerület, míg \(\displaystyle c\) a \(\displaystyle C\)-vel szemközti oldal hossza).
Gyakran használt tény az is, hogy egy \(\displaystyle C\)-nél derékszögű háromszög esetében \(\displaystyle CB_1IA_1\) egy négyzet, hiszen \(\displaystyle C\)-nél, \(\displaystyle B_1\)-nél és \(\displaystyle A_1\)-nél (és így \(\displaystyle I\)-nél is) is derékszöge van, és van olyan szomszédos oldalpárja, amely egyenlő, pl. \(\displaystyle IA_1 = IB_1 = r\), \(\displaystyle CA_1 = CB_1 = s-c\). Ebből azt kapjuk, hogy
\(\displaystyle r = s - c. \)
Az \(\displaystyle r\) helyére \(\displaystyle (s-c)\)-t helyettesítve a bizonyítandó állításban:
$$\begin{eqnarray*} 2(s-c)^2 &=& (c-a)(c-b), \\ 4(s-c)^2 &=& 2(c-a)(c-b), \\ (a+b-c)^2 &=& 2(c-a)(c-b), \\ a^2 + b^2 + c^2 + 2ab - 2c(a+b), &=& 2c^2 + 2ab - 2c(a+b), \\ a^2 + b^2 &=& c^2. \end{eqnarray*}$$Ekvivalens átalakításokat végeztünk, és az utolsó egyenlőség biztosan teljesül, hiszen épp ezt állítja a Pitagorasz-tétel.
Statisztika:
A B. 5495. feladat értékelése még nem fejeződött be.
A KöMaL 2025. decemberi matematika feladatai

