A B. 5501. feladat (2025. december)

B. 5501. Az \(\displaystyle ABC\) háromszög beírt köre a \(\displaystyle BC\), \(\displaystyle CA\), \(\displaystyle AB\) oldalakat rendre a \(\displaystyle D, E, F\) pontokban érinti, az \(\displaystyle F\) ponttal átellenes pont a beírt körön \(\displaystyle G\). A \(\displaystyle GD\) és \(\displaystyle GE\) egyenesek az \(\displaystyle AB\) egyenest a \(\displaystyle D'\), illetve \(\displaystyle E'\) pontokban metszik. Mutassuk meg, hogy az \(\displaystyle AED'\) és \(\displaystyle BDE'\) körök a beírt körön metszik egymást.

Javasolta: Jármai Roland (Budapest)

(6 pont)

A beküldési határidő 2026. január 12-én LEJÁRT.

Megoldás. Legyen az \(\displaystyle AB\) oldalhoz hozzáírt kör középpontja \(\displaystyle J\), érintési pontja az \(\displaystyle AB\) egyenesen \(\displaystyle H\), a \(\displaystyle JF\) egyenes és a beírt kör második metszéspontja \(\displaystyle P\ne F\). Azt állítjuk, hogy az \(\displaystyle AED'\) és \(\displaystyle BDE'\) körök átmennek a \(\displaystyle J\) és a \(\displaystyle P\) pontokon, utóbbi bizonyítja a feladat állítását.

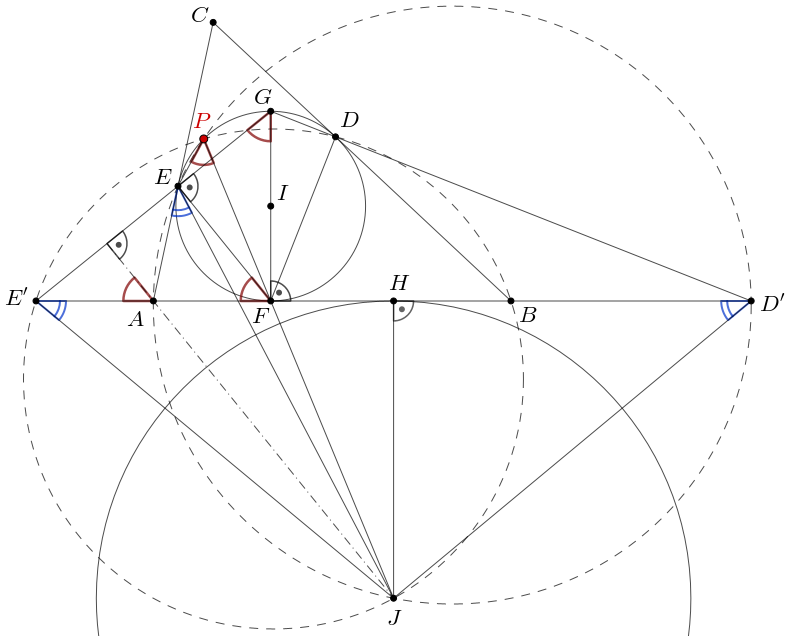
Az \(\displaystyle AED'\) és \(\displaystyle BDE'\) körök szerepe szimmetrikus, így elég azt igazolni, hogy \(\displaystyle J\) és \(\displaystyle P\) is az \(\displaystyle AED'\) körön van.

A beírt körben \(\displaystyle FG\) átmérő, tehát a Thalész-tétel miatt \(\displaystyle EF\perp EG\). Ezért az \(\displaystyle EE'F\) háromszög derékszögű. A beírt körhöz az \(\displaystyle A\) pontból húzott \(\displaystyle AE\) és \(\displaystyle AF\) érintők egyenlők, így az \(\displaystyle A\) pont a \(\displaystyle EF\) befogó felezőmerőlegesének és az \(\displaystyle E'F\) átfogónak a metszéspontja, ami az átfogó felezőpontja, egyben a háromszög köré írt kör középpontja. Ezért \(\displaystyle AF=AE=AE'\).

A \(\displaystyle J\) pont az \(\displaystyle AB\) oldalhoz hozzáírt kör középpontja, emiatt az \(\displaystyle AJ\) egyenes a \(\displaystyle BAC\sphericalangle\) külső felezője, egyben az \(\displaystyle EAE'\sphericalangle\) felezője. Mivel \(\displaystyle AE=AE'\), az \(\displaystyle AE'JE\) négyszög deltoid, \(\displaystyle JA\) az \(\displaystyle EE'\) szakasz felezőmerőlegese, és \(\displaystyle AEJ\sphericalangle =JE'A\sphericalangle\).

Jól ismert, hogy (az \(\displaystyle ABC\) háromszög oldalaival és félkerületével kifejezve) \(\displaystyle AF=BH=s-a\) és \(\displaystyle BF=AH=s-b\), ezért \(\displaystyle E'H=E'A+AH=AF+AH=BH+BF=BH+D'B=D'H\), vagyis \(\displaystyle H\) a \(\displaystyle D'E'\) szakasz felezőpontja. A hozzáírt kör \(\displaystyle JH\) sugara merőleges az \(\displaystyle AB\) érintőre, így a \(\displaystyle D'E'J\) háromszög egyenlő szárú, és \(\displaystyle JE'D'\sphericalangle=E'D'J\sphericalangle\).

Ezek után \(\displaystyle AEJ\sphericalangle =JE'A\sphericalangle= JE'D'\sphericalangle= E'D'J\sphericalangle= AD'J\sphericalangle\) miatt az \(\displaystyle AED'\) kör átmegy a \(\displaystyle J\) ponton.

Ha \(\displaystyle P\) a beírt kör \(\displaystyle G\)-t tartalmazó \(\displaystyle FE\) ívén van, akkor \(\displaystyle EPJ\sphericalangle= EPF\sphericalangle= EFE'\sphericalangle= 180^\circ-E'AJ\sphericalangle= 180^\circ-JAE\sphericalangle\) miatt az \(\displaystyle AED'=AEJ\) kör a \(\displaystyle P\) ponton is átmegy. Ha \(\displaystyle P\) a \(\displaystyle G\)-t nem tartalmazó \(\displaystyle EF\) ívre esik, akkor \(\displaystyle JPE\sphericalangle= FPE\sphericalangle= 180^\circ-EFE'\sphericalangle= E'AJ\sphericalangle= JAE\sphericalangle\) miatt miatt megy át az \(\displaystyle AED'J\) kör a \(\displaystyle P\) ponton. Ha pedig \(\displaystyle P=E\), akkor pedig \(\displaystyle P\) emiatt is \(\displaystyle AED'J\) körön van.

Statisztika:

A B. 5501. feladat értékelése még nem fejeződött be.

A KöMaL 2025. decemberi matematika feladatai