A C. 1052. feladat (2010. november)

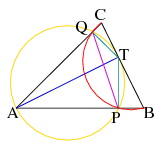
C. 1052. Az ABC hegyesszögű háromszög A csúcsából merőlegest állítunk a BC oldalra, ennek talppontja T. T-ből merőlegest állítunk az AB és AC oldalakra, ezek talppontjai P és Q.

Bizonyítsuk be, hogy BPQC négyszög húrnégyszög.

(5 pont)

A beküldési határidő 2010. december 10-én LEJÁRT.

Megoldás. Mivel az \(\displaystyle APT\) és \(\displaystyle ATQ\) háromszögek derékszögűek és közös az (\(\displaystyle AT\)) átfogójuk, ezért a köréjük írt (Thalész) kör egybeesik. Úgy is mondhattuk volna, hogy az \(\displaystyle APTQ\) négyszög húrnégyszög, mert a szemközt levő szögeik (feladat szerint \(\displaystyle AT\)-tól különböző félsíkban vannak) összege \(\displaystyle 90^\circ + 90^\circ =180^\circ\). Felhasználva, hogy adott sugarú kör azonos hosszúságú íveihez (v. húrokhoz) tartozó középponti szögek nagysága megegyezik. Így \(\displaystyle TPQ\angle =TAQ\angle = 90^\circ - \gamma\). A vizsgálandó \(\displaystyle BCQP\) négyszögben \(\displaystyle QPB\angle + BCQ\angle = (90^\circ - \gamma + 90^\circ) + \gamma = 180^\circ\), azaz a \(\displaystyle BCPQ\) négyszög húrnégyszög.

Statisztika:

181 dolgozat érkezett.
5 pontot kapott:	101 versenyző.
4 pontot kapott:	37 versenyző.
3 pontot kapott:	18 versenyző.
2 pontot kapott:	10 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	7 versenyző.
Nem versenyszerű:	4 dolgozat.

A KöMaL 2010. novemberi matematika feladatai