A C. 1223. feladat (2014. március)

C. 1223. Egy szabályos négyoldalú gúla oldallapjai egyenlő oldalú háromszögek. Mekkora a gúla szomszédos oldallapjainak hajlásszöge?

(5 pont)

A beküldési határidő 2014. április 10-én LEJÁRT.

Megoldás. Legyen a gúla minden éle \(\displaystyle a\) hosszúságú. Tekintsük az \(\displaystyle ABE\) és a \(\displaystyle CBE\) lapot, az \(\displaystyle EB\) él felezőpontja legyen \(\displaystyle F\). Mivel \(\displaystyle AF\perp EB\) és \(\displaystyle CF\perp EB\), ezért a két lap hajlásszöge az \(\displaystyle AFC\angle\), melyet jelöljön \(\displaystyle \alpha\).

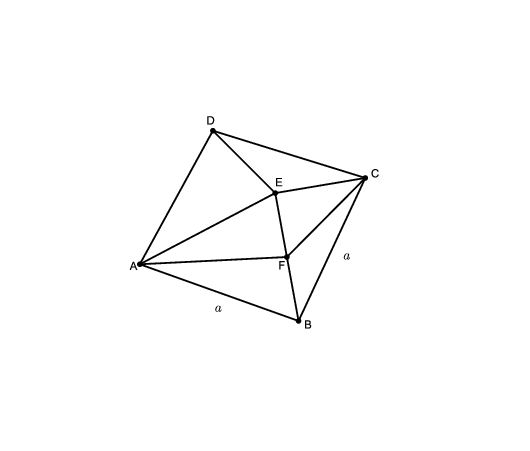
Tekintsük az \(\displaystyle AFC\) háromszöget. Mivel \(\displaystyle AC\) az alaplap átlója, ezért hossza \(\displaystyle \sqrt2a\). A másik két oldal pedig az \(\displaystyle a\) oldalú szabályos háromszög magassága, ezért mindkettő \(\displaystyle \frac{\sqrt3}{2}a\) hosszú.

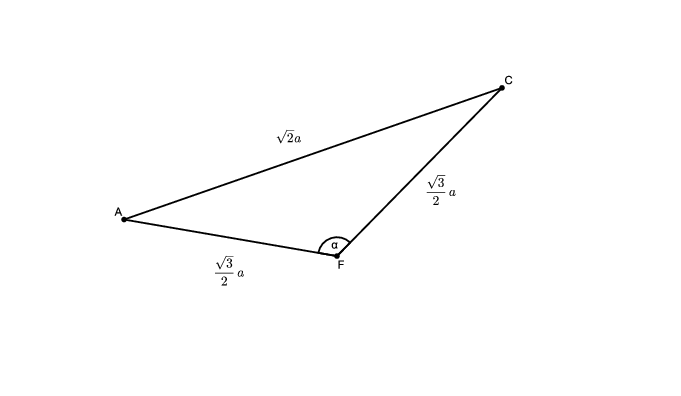
Írjuk fel az \(\displaystyle AFC\) háromszögben a koszinusz-tételt:

\(\displaystyle (\sqrt2a)^2=\left(\frac{\sqrt3}{2}a\right)^2+\left(\frac{\sqrt3}{2}a\right)^2 -2\cdot\frac{\sqrt3}{2}a\cdot\frac{\sqrt3}{2}a\cdot\cos\alpha,\)

mindkét oldalt osztva \(\displaystyle a^2\neq0\)-val majd rendezve:

\(\displaystyle 2=\frac34+\frac34-\frac32\cos\alpha,\)

\(\displaystyle \frac12=-\frac32\cos\alpha,\)

\(\displaystyle \cos\alpha=-\frac13,\)

amiből, mivel \(\displaystyle 0<\alpha<180^{\circ}\):

\(\displaystyle \alpha\approx109,47^{\circ}.\)

Tehát a gúla két szomszédos oldallapjának hajlásszöge \(\displaystyle \approx109,47^{\circ}\).

Statisztika:

41 dolgozat érkezett.
5 pontot kapott:	Bajnok Anna, Beke 997 Tamás, Bereczki Zoltán, Bögös Dániel, Chourfi Abdel Karim, Demeter Dániel, Denke Dorottya, Dombrovszky Borbála, Farkas Dóra, Gnandt Balázs, Jójárt Alexandra, Kranczler Dóra, Paulovics Zoltán, Szabó 157 Dániel, Szabó 524 Tímea, Temesvári Fanni, Zsiros Ádám.
4 pontot kapott:	Fényes Balázs, Ficsor Enikő, Hegel Patrik, Hegyi Zoltán, Kenderes Anett, Kovács 599 Bálint, Rimóczi Alma, Semegi Judit, Somogyi Zoltán, Sziegl Benedek, Szűcs Dorina, Szvetnik Ákos, Tekeli Miklós, Telek Máté László, Tóth Zsófia, Zhorela Viktor.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	2 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2014. márciusi matematika feladatai