A C. 1395. feladat (2017. január)

C. 1395. Az \(\displaystyle ABCD\) paralelogramma egyik oldala kétszerese a másiknak. Adjuk meg a belső szögfelezők által meghatározott paralelogramma és \(\displaystyle ABCD\) területének arányát.

(5 pont)

A beküldési határidő 2017. február 10-én LEJÁRT.

Megoldás. Felezzük meg a paralelogramma hosszabb oldalait. Az ábra jelöléseit használva, legyen az \(\displaystyle AB\) oldal felezőpontja \(\displaystyle E\), a \(\displaystyle DC\) oldalé pedig \(\displaystyle F\). \(\displaystyle EF\) a paralelogramma középvonala, így \(\displaystyle AD=EF=BC\) és \(\displaystyle AD||EF||BC\).

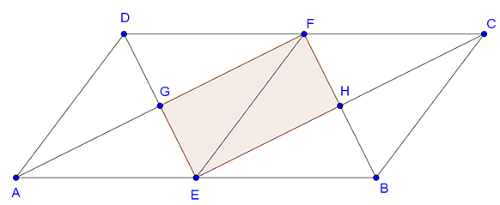
Ezért az \(\displaystyle EF\) szakasz a paralelogrammát két rombuszra osztja, hiszen \(\displaystyle AE=AD\) és \(\displaystyle EB=BC\) és a szemközti oldalak párhuzamosak. A paralelogramma belső szögfelezői egyben az \(\displaystyle AEFD\) és \(\displaystyle BCFE\) rombuszok átlói, mivel a rombusz átlói szögfelezők. Az átlók, vagyis a szögfelezők mindkét rombuszon belül merőlegesek egymásra és a rombuszokat 4-4 db egybevágó derékszögű háromszögre bontják. Így a paralelogramma 8 db ilyen háromszögből áll. A szögfelezők által meghatározott \(\displaystyle EHFG\) paralelogramma téglalap, és 2 db ilyen derékszögű háromszögből áll.

Tehát az \(\displaystyle EHFG\) és az \(\displaystyle ABCG\) paralelogrammák területének aránya: \(\displaystyle \frac 28=\frac 14\).

Statisztika:

209 dolgozat érkezett.
5 pontot kapott:	184 versenyző.
4 pontot kapott:	12 versenyző.
3 pontot kapott:	1 versenyző.
1 pontot kapott:	8 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2017. januári matematika feladatai