A C. 1491. feladat (2018. szeptember)

C. 1491. Az $\displaystyle ABCD$ téglalap $\displaystyle AD$ oldala $\displaystyle 1$ cm hosszú. A $\displaystyle BAD$ szög szögfelezője és az $\displaystyle AC$ átló felező merőlegese a $\displaystyle CD$ oldalon metszi egymást. Adjuk meg a $\displaystyle CD$ oldal pontos értékét.

(5 pont)

A beküldési határidő 2018. október 10-én LEJÁRT.

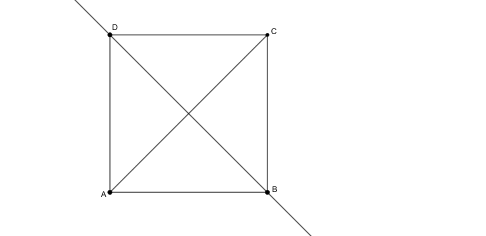
Megoldás. Ha $\displaystyle AD=AB$, akkor a szögfelező egybeesik az $\displaystyle AC$ átlóval, aminek a felező merőlegese a $\displaystyle D$ pontban metszi a $\displaystyle CD$ oldalt.

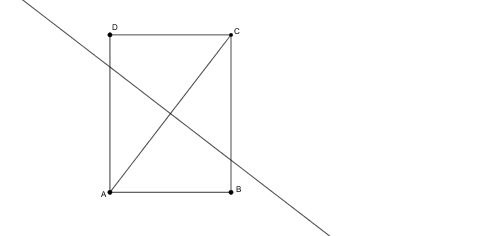
Ha $\displaystyle AD>AB$, akkor az oldalfelező merőleges nem metszi a $\displaystyle CD$ szakaszt.

Legyen tehát $\displaystyle AD<AB$ (ekkor a szögfelező az átló ,,felett" halad) és használjuk az ábra jelöléseit. Az $\displaystyle AC$ átló felezőpontja legyen $\displaystyle F$, a $\displaystyle BAD∡$ szögfelezőjének és az $\displaystyle AC$ átló felező merőlegesének metszéspontja pedig $\displaystyle M$.

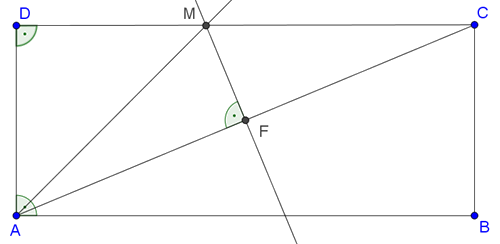
$\displaystyle DAM∡=45°$, ezért $\displaystyle ADM$ egyenlő szárú derékszögű háromszög: $\displaystyle DM=AD=1$ cm. A háromszög átfogója pedig $\displaystyle AM=\sqrt2$ cm.

Az $\displaystyle AC$ átló $\displaystyle FM$ felező merőlegese szimmetriatengely az $\displaystyle AMC$ háromszögben, ezért $\displaystyle MC=AM=\sqrt2$.

Mivel az $\displaystyle M$ pont a $\displaystyle DC$ oldalra esik, így $\displaystyle DC=DM+MC=1+\sqrt2$.

Tehát a $\displaystyle CD$ oldal pontos értéke: $\displaystyle 1+\sqrt2$ cm.

Statisztika:

268 dolgozat érkezett.
5 pontot kapott:	207 versenyző.
4 pontot kapott:	33 versenyző.
3 pontot kapott:	7 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	10 dolgozat.

A KöMaL 2018. szeptemberi matematika feladatai