A C. 1523. feladat (2019. január)

C. 1523. Egy konvex négyszöget az átlóival háromszögekre bontunk. Mutassuk meg, hogy ha a négy háromszög területei között pontosan háromféle érték fordul elő, akkor a négyszög trapéz.

(5 pont)

A beküldési határidő 2019. február 11-én LEJÁRT.

Megoldás. Az, hogy a területek között pontosan háromféle érték fordul elő, úgy is megfogalmazható, hogy pontosan két háromszögnek egyenlő a területe.

1. eset: Két szomszédos háromszögnek egyenlő a területe:

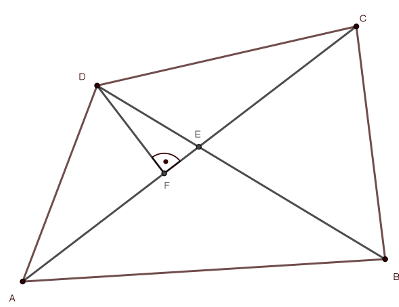
Legyen például \(\displaystyle AED\) és \(\displaystyle ECD\) háromszög területe egyenlő (bármely 2 szomszédos háromszögre ugyanez az érvelés alkalmazható). Ezen két háromszög \(\displaystyle D\) csúcsból induló magassága közös (hiszen a \(\displaystyle D\)-vel szemközti oldaluk egy egyenesbe esik), ekkor viszont a \(\displaystyle D\)-vel szemközti oldaluk is egyenlő hosszú, azaz \(\displaystyle AE=EC\). Ám ekkor hasonló érvelést alkalmazva kapjuk, hogy az \(\displaystyle ABE\) háromszög területe egyenlő az \(\displaystyle EBC\) háromszög területével, azaz csak kétféle terület érték fordulhatna elő, ami ellentmondás.

2. eset: Két szemközti háromszög területe egyenlő:

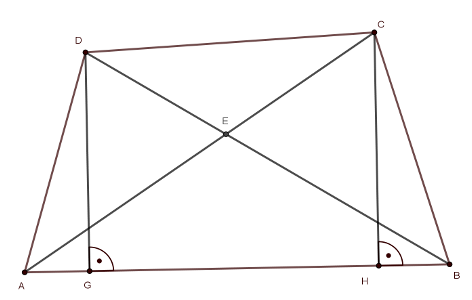
Legyen az \(\displaystyle AED\) és az \(\displaystyle EBC\) háromszögek területe egyenlő (a másik 2 szemközti háromszöggel ugyanez elmondható). Ekkor nyilvánvalóan az \(\displaystyle ABD\) és \(\displaystyle ABC\) háromszögek területe is egyenlő. Ennek a két háromszögnek \(\displaystyle AB\) közös oldala, így az \(\displaystyle AB\)-hez tartozó magasságuk hosszának egyenlőnek kell lennie: \(\displaystyle DG=CH\). Ez azt jelenti, hogy \(\displaystyle AB \parallel CD\), azaz a négyszögünk valóban trapéz.

Ezzel a feladat állítását igazoltuk.

Statisztika:

63 dolgozat érkezett.
5 pontot kapott:	Ajtai Boglárka, Borzon Márton, Cseke Tibor123, Debreczeni Tibor, Draskóczi Dóra Boglárka, Éberle Richárd, Forgács Kata, Gál Bence, Gálffy Veronika, Gárgyán Barnabás, Hordós Adél Zita, Horváth 713 Alíz, Jankovits András, Kis 194 Károly, Kis-Tóth Janka, Kubik Emese, Majerusz Ádám, Mészáros 916 Márton, Molnár 410 István, Nyitrai Boglárka, Rozgonyi Gergely, Sal Dávid, Schäffer Tamás, Sebe Anna, Szabó 677 Balázs István, Szabó 808 Álmos Levente, Szalontai Kinga Sára, Székelyhidi Klára, Szigeti Donát, Tóth Benedek, Varga Ákos, Wagner Dávid Barnabás.
4 pontot kapott:	Facskó Vince, Falvay Júlia, Kim 666 Levente, Rátki Luca, Vándorffy Áron.
3 pontot kapott:	6 versenyző.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	4 versenyző.
Nem versenyszerű:	2 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	3 dolgozat.

A KöMaL 2019. januári matematika feladatai