A C. 1561. feladat (2019. október)

C. 1561. Mekkorák lehetnek egy háromszög szögei, ha a háromszögbe írt kör érintési pontjai által meghatározott háromszög hasonló az eredetihez?

(5 pont)

A beküldési határidő 2019. november 11-én LEJÁRT.

Megoldás. Használjuk az ábra jelöléseit, a kiindulási háromszög \(\displaystyle ABC\), szögei \(\displaystyle \alpha,\beta,\gamma\).

A feladat szövege alapján az \(\displaystyle ABC\) és \(\displaystyle DEF\) háromszög hasonló, azaz a \(\displaystyle DEF\) háromszög szögei is \(\displaystyle \alpha, \beta, \gamma\) valamilyen sorrendben.

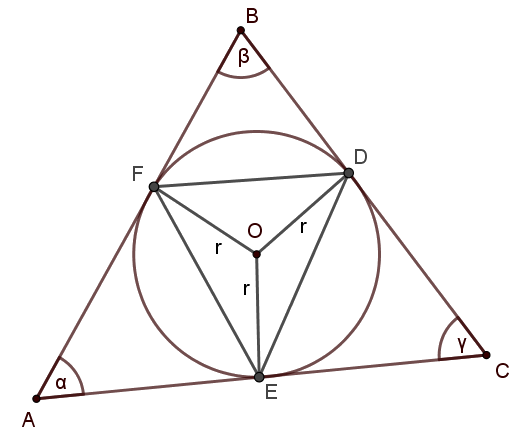
Először jegyezzük meg, hogy \(\displaystyle OFB \angle = ODB \angle= 90^\circ\), mert egy körhöz húzott külső érintő merőleges az érintési pontba húzott sugárra. Ekkor az \(\displaystyle ODBF\) négyszöget nézve kapjuk, hogy \(\displaystyle FOD \angle= 360^\circ - 2 \cdot 90^\circ- \beta = \alpha + \gamma.\) Mivel az \(\displaystyle OFD\) háromszög egyenlőszárú (két oldala sugár a beírt körben), így \(\displaystyle OFD \angle= ODF \angle = (180^\circ - (\alpha + \gamma))/2= \beta/2.\) Hasonlóan belátható, hogy az \(\displaystyle EFO\), illetve \(\displaystyle EDO\) egyenlőszárú háromszögek szárszögei rendre \(\displaystyle \alpha/2\), illetve \(\displaystyle \gamma/2\). Vagyis azt kaptuk, hogy az \(\displaystyle FED\) háromszög szögei \(\displaystyle \alpha/2+ \beta/2, \alpha/2+ \gamma/2, \beta/2+ \gamma/2\).

A feltétel szerint a \(\displaystyle DEF\) háromszög szögei \(\displaystyle \alpha,\beta,\gamma\). A szimmetria miatt feltehetjük, hogy \(\displaystyle \alpha\le\beta\le\gamma\), ekkor \(\displaystyle 90^\circ-\tfrac\gamma2\le90^\circ-\tfrac\beta2\le90^\circ-\tfrac\alpha2\), emiatt egyértelmű, hogy melyik szög melyik szöggel egyenlő: \(\displaystyle 90^\circ-\tfrac\gamma2=\alpha\), \(\displaystyle 90^\circ-\tfrac\beta2=\beta\) és \(\displaystyle 90^\circ-\tfrac\alpha2=\gamma\). A második egyenlőségből rögtön adódik, hogy \(\displaystyle 90^{\circ}=\frac32\beta\), vagyis \(\displaystyle \beta=60^{\circ}\). Az elsőből és a harmadikból pedig \(\displaystyle 90^{\circ}=\alpha+\frac{\gamma}{2}=\gamma+\frac{\alpha}{2}\), amiből \(\displaystyle \alpha/2/=\gamma/2\), azaz \(\displaystyle \alpha=\gamma\). Mivel \(\displaystyle \alpha+\gamma=180^{\circ}-\beta=120^{\circ}\), ebből már következik, hogy \(\displaystyle \alpha=\gamma=60^{\circ}\).

Tehát a feladatban szereplő háromszög mindhárom szöge \(\displaystyle 60^\circ\)-os, a háromszög szabályos.

Statisztika:

144 dolgozat érkezett.
5 pontot kapott:	Albert Ákos, Balázs Réka, Bana Marcell, Bánó Bulcsú, Barczikay Ákos, Cserkuti Sándor, Domján Olivér, Feczkó Nóra, Fekete Patrik, Foris Dávid, Fórizs Botond, Gombos Gergely , Görömbey László, Hajós Balázs, Halász Henrik, Hegedűs András , Horváth Milán, Kalocsai Zoltán, Kocsis 827 Péter, Kovács Benedek Noel, Kun Timon, Kurucz Kitti, László Gergely, Lőw László, Márky Anna, Mátéfy Ádám , Metzger Ábris András, Nagy 989 Lea, Németh László Csaba, Németh Máté Előd, Perényi Lídia , Reviczki Roland, Sárvári Borka Luca, Sebestyén József Tas, Somogyi Dalma, Szabó 219 Petra, Szalanics Tamás, Szalay Réka, Szirmai Dénes, Téglás Panna.
4 pontot kapott:	19 versenyző.
3 pontot kapott:	31 versenyző.
2 pontot kapott:	8 versenyző.
1 pontot kapott:	14 versenyző.
0 pontot kapott:	27 versenyző.
Nem versenyszerű:	5 dolgozat.

A KöMaL 2019. októberi matematika feladatai