A C. 991. feladat (2009. május)

C. 991. A 3, 4, 5 oldalú derékszögű háromszöget az átfogóra merőleges egyenessel szétvágjuk egy érintőnégyszögre és egy derékszögű háromszögre. Határozzuk meg a négyszög oldalainak hosszát.

(5 pont)

A beküldési határidő 2009. június 15-én LEJÁRT.

Megoldás. Legyen a=3, b=4, c=5.

1.eset: Az egyenes a b oldalt metszi a Q_b pontban.

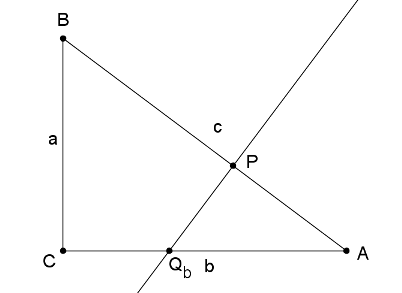
Legyen BP=x, ekkor PA=5-x. Mivel $AQ_bP\triangle\approx ABC\triangle$ , ezért $\frac{PQ_b}{5-x}=\frac34~\Rightarrow~PQ_b=\frac34(5-x)$ és $\frac{Q_bA}{5-x}=\frac54~\Rightarrow~Q_bA=\frac54(5-x)$ .

Ekkor $CQ_b=4-\frac54(5-x)=\frac{5x-9}{4}$ .

Mivel BCQ_bP érintőnégyszög, azért BC+Q_bP=CQ_b+PB, azaz $3+\frac34(5-x)=\frac{5x-9}{4}+x$ , ebből x=3.

Tehát a négyszög oldalai 3; 1,5; 1,5; 3.

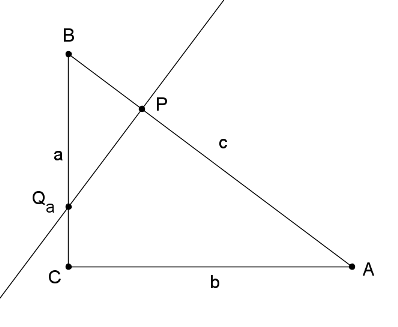
2. eset: Az egyenes az a oldalt metszi a Q_a pontban. Legyen AP=x, ekkor PB=5-x. Mivel $BQ_aP\triangle\approx BAC\triangle$ , ezért $\frac{PQ_a}{5-x}=\frac43~\Rightarrow~PQ_a=\frac43(5-x)$ és $\frac{Q_aB}{5-x}=\frac53~\Rightarrow~Q_aB=\frac53(5-x)$ .

Ekkor $CQ_a=3-\frac53(5-x)=\frac{5x-16}{3}$ .

Mivel APQ_aC érintőnégyszög, azért AC+Q_aP=CQ_a+PA, $4+\frac43(5-x)=\frac{5x-16}{3}+x$ , ebből x=4.

Tehát a négyszög oldalai 4; $\frac43$ ; $\frac43$ ; 4.

Statisztika:

122 dolgozat érkezett.

5 pontot kapott: 76 versenyző.

4 pontot kapott: 5 versenyző.

3 pontot kapott: 29 versenyző.

2 pontot kapott: 8 versenyző.

1 pontot kapott: 3 versenyző.

Nem versenyszerű: 1 dolgozat.

A KöMaL 2009. májusi matematika feladatai

122 dolgozat érkezett.
5 pontot kapott:	76 versenyző.
4 pontot kapott:	5 versenyző.
3 pontot kapott:	29 versenyző.
2 pontot kapott:	8 versenyző.
1 pontot kapott:	3 versenyző.
Nem versenyszerű:	1 dolgozat.

Már regisztráltál?
Új vendég vagy?