 |
Az I. 657. feladat (2025. március) |
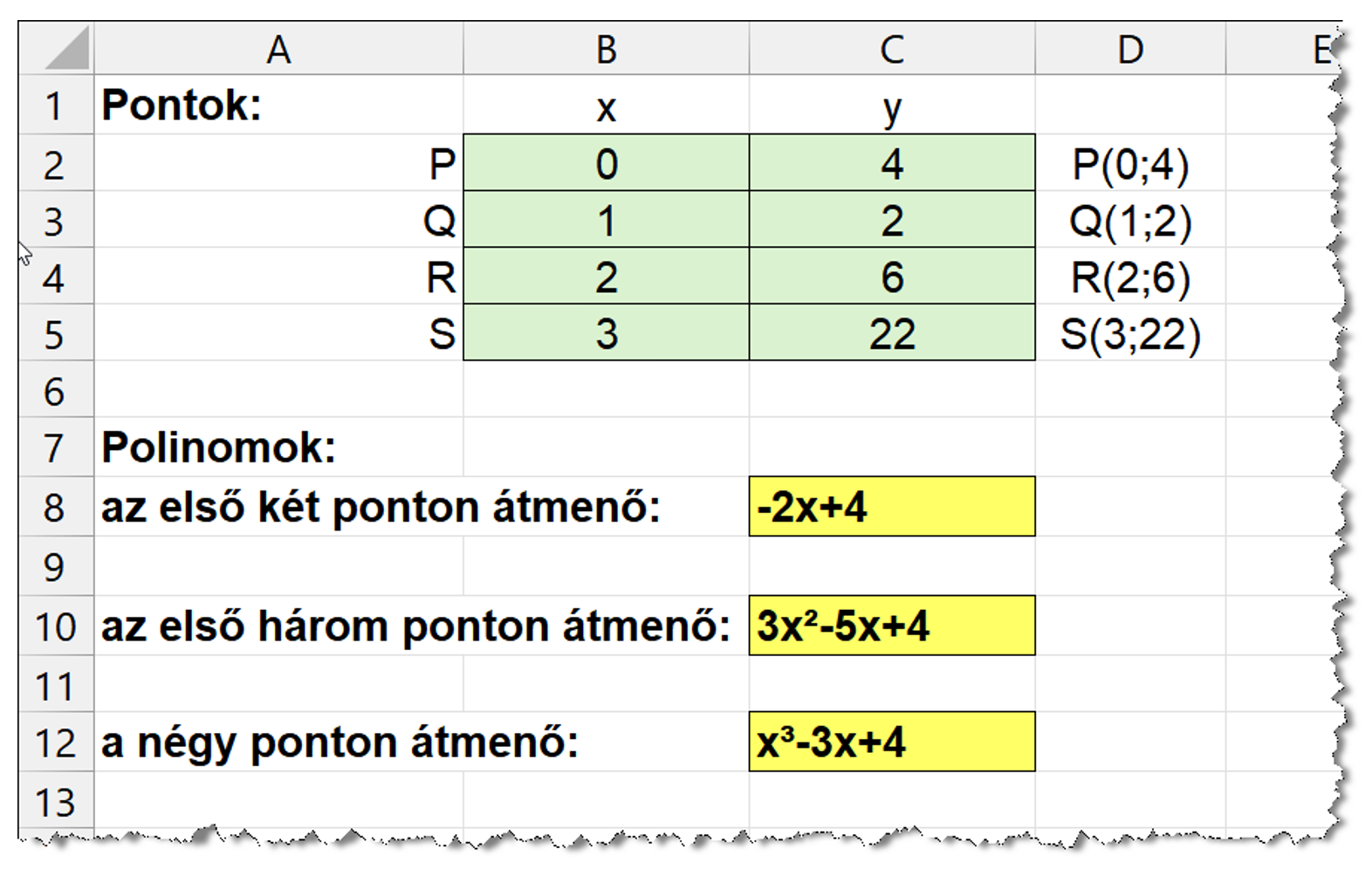
I. 657. Legyen a sík négy, különböző \(\displaystyle x\)-koordinátájú pontja \(\displaystyle P(p_x;p_y)\), \(\displaystyle Q(q_x;q_y)\), \(\displaystyle R(r_x;r_y)\) és \(\displaystyle S(s_x;s_y)\). Számítsuk ki a négy pont közül az első kettőn, az első hármon, illetve a négy ponton átmenő legfeljebb első-, másod-, illetve harmadfokú polinom együtthatóit.
- Nyissunk meg egy üres táblázatkezelő munkafüzetet. Készítsük el az alapadatok beviteli területét és az eredmény kijelzőjét a minta szerint.
- A munkalap betűtípusa Arial legyen, a betűméret 11 pont.
- A cellák igazítása, szegélyezése, kitöltőszíne kövesse a mintát.
- A D2:D5 tartományban a pontok koordinátáinak begépelése után jelenjenek meg a koordináták is, ahogy az a további mintákon látszik.
- Ha mind a nyolc cella a feltételeknek megfelelő számadatot tartalmaz, kezdődhet a polinomok generálása.
- A C8 cellában megjelenő polinomnak akkor kell helyesnek lennie, ha a B2:C3 tartomány mind a négy cellája tartalmaz a feltételeknek megfelelő értéket.
- A C10 cellában megjelenő polinomnak akkor kell helyesnek lennie, ha a B2:C4 tartomány mind a hat cellája tartalmaz a feltételeknek megfelelő értéket.
- A C12 cellában megjelenő polinomnak akkor kell helyesnek lennie, ha a B2:C5 tartomány mind a nyolc cellája tartalmaz a feltételeknek megfelelő értéket.
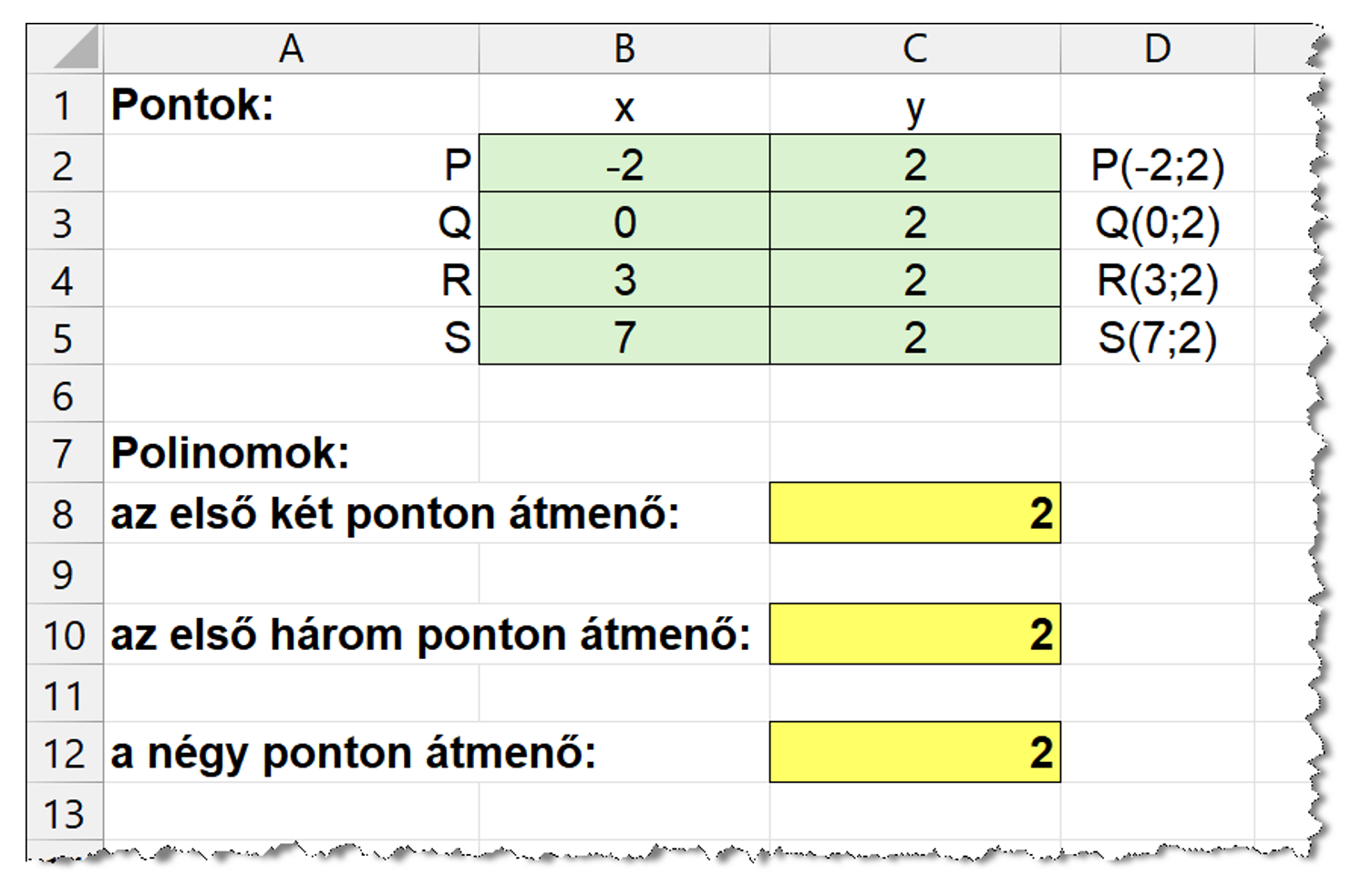
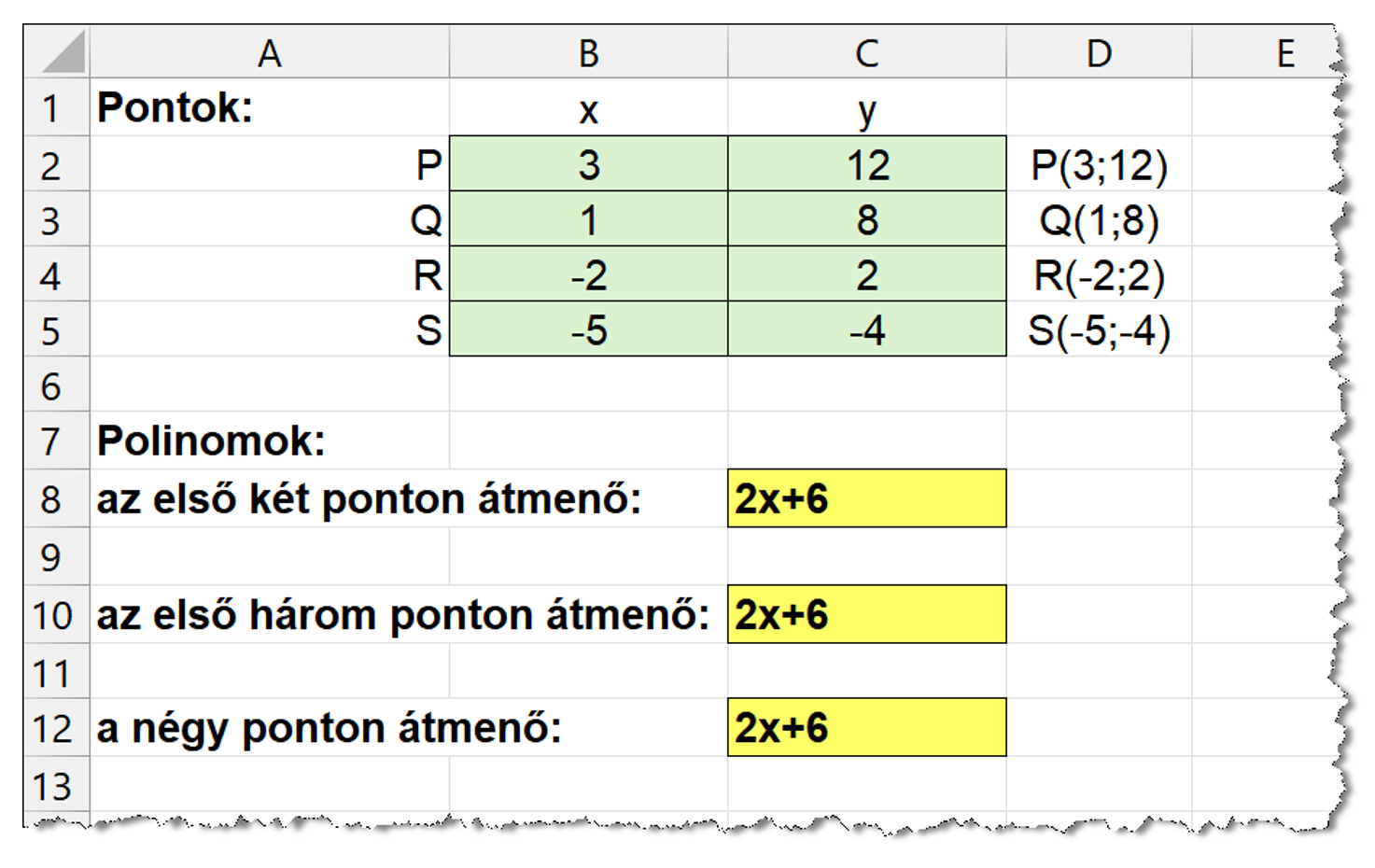
- Persze a pontok speciális elhelyezkedése miatt kijöhet olyan eredmény, hogy nincs elsőfokú, másodfokú, esetleg harmadfokú polinom sem.
- A polinomok kövessék a hagyományos matematikai leírás szabályait. Nem szabályos leírása a polinomoknak például: \(\displaystyle -1x^2++7\), vagy \(\displaystyle +0x^3+1x+0\), vagy \(\displaystyle 0x^2+-1\).
- Segítségül még annyit, hogy
- egy \(\displaystyle n\)-edfokú polinomnak maximum n zérushelye van, továbbá
- törzstényezős felbontás nem csak a másodfokú polinomoknál létezik.
Segédszámításokat a 14. sortól kezdve végezhetünk. A megoldásban saját függvény vagy makró nem használható.
Beküldendő egy tömörített i657.zip állományban a táblázatkezelő munkafüzet, illetve egy rövid dokumentáció, amelyben részletesen szerepel a megoldási módszer, a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.
(10 pont)
A beküldési határidő 2025. április 15-én LEJÁRT.
Statisztika:
Az I. 657. feladat értékelése még nem fejeződött be.
A KöMaL 2025. márciusi informatika feladatai