 |
Az I. 660. feladat (2025. április) |
I. 660. Nevezzük \(\displaystyle K\)-nak az origó középpontú, \(\displaystyle 10\;000\) egység sugarú körlap I. síknegyedbe eső részét. Matematikai formalizmussal: az \(\displaystyle x\geq 0\) és \(\displaystyle y\geq 0\) és \(\displaystyle x^2+y^2\leq 10\;000^2\) feltételekkel adott ponthalmaz.
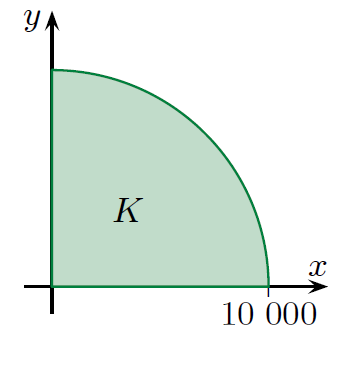
Feladataink:
- Nyissunk meg egy üres táblázatkezelő munkafüzetet, nevezzük át a munkalapot negyedkor névre, a munkafüzetet mentsük pontok néven. Segédszámításokat csak ezen a munkalapon végezzünk a 9. sor alatt.
- Hozzunk létre egy üres munkalapot segedadatok néven. Illesszük be az A1 cellától az UTF-8 kódolású, tabulátorokkal tagolt segedadatok.txt fájl tartalmát és formázzuk meg a minták szerint:
- Hány rácspont (vagyis olyan pont, amelynek mindkét koordinátája egész szám) van \(\displaystyle K\) belsejében? (A1)
- Hány olyan rácspont van \(\displaystyle K\) belsejében, amelyiknek mindkét koordinátája négyzetszám? (A2)
- Hány olyan rácspont van \(\displaystyle K\) belsejében, amelyiknek mindkét koordinátája köbszám? (A3)
- Hány olyan rácspont van \(\displaystyle K\) belsejében, amelyiknek mindkét koordinátája prímszám? (A4)
- Hány olyan rácspont van \(\displaystyle K\) belsejében, amelyiknek x koordinátája prímszám, \(\displaystyle y\) koordinátája négyzetszám? (A5)
- Melyik az a legkisebb, egész értékű r sugár, amely esetén a \(\displaystyle K\)-hoz hasonlóan elhelyezkedő \(\displaystyle r\) sugarú \(\displaystyle k\) negyedkör belsejében a fenti első négy feltételnek eleget tevő pontokból mind a négy feltétel esetén legalább \(\displaystyle 100\)-\(\displaystyle 100\) pont van? (A6)
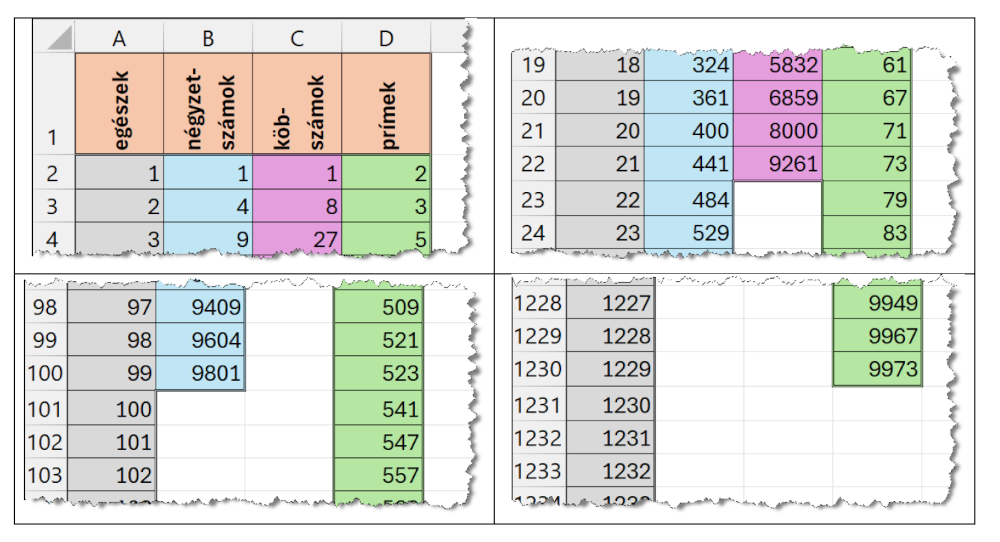
Számítsuk ki a választ a következő kérdésekre és jelenítsük meg az eredményt a zárójelben jelölt cellában:
Segédszámításokat a negyedkor munkalapon a 9. sor alatt lehet végezni. A megoldásban saját függvény vagy makró nem használható.
Beküldendő az i660.zip tömörtett állományban a munkafüzet és egy rövid dokumentáció, amelyben szerepel a számítások magyarázata, a táblázatkezelő neve és verziószáma.
Letölthető fájl: segedadatok.txt
(10 pont)
A beküldési határidő 2025. május 15-én LEJÁRT.
Bence Mátyás kiemeledő munkája: Pontok.xlsx
Statisztika:
12 dolgozat érkezett. 10 pontot kapott: Bencze Mátyás, Gyönki Dominik. 6 pontot kapott: 1 versenyző. 5 pontot kapott: 1 versenyző. 4 pontot kapott: 1 versenyző. 2 pontot kapott: 4 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2025. áprilisi informatika feladatai
