A K/C. 882. feladat (2025. december)

K/C. 882. Egy \(\displaystyle ABCDEFGHIJKL\) szabályos tizenkétszög \(\displaystyle AC\) és \(\displaystyle FH\) átlójára befelé egy-egy négyzetet írunk. Mutassuk meg, hogy a két négyzetnek van egy közös csúcsa.

(5 pont)

A beküldési határidő 2026. január 12-én LEJÁRT.

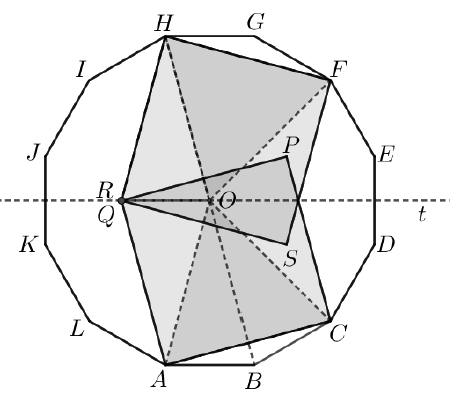
Megoldás. A szabályos tizenkétszög középpontja legyen \(\displaystyle O\). Az \(\displaystyle OAC\) és \(\displaystyle OFH\) szabályos háromszögek, mert \(\displaystyle OA=OC=OF=OH=r\), a tizenkétszög köré írt kör sugara, illetve például \(\displaystyle AOC\sphericalangle=\dfrac{360^{\circ}}{12}\cdot2=60^{\circ}\).

Az \(\displaystyle AC\) átlóra írt négyzet legyen \(\displaystyle ACPQ\), az \(\displaystyle FH\) átlóra írt négyzet legyen \(\displaystyle FHRS\). Szeretnénk belátni, hogy \(\displaystyle Q=R\). Mivel az ábra szimmetrikus a \(\displaystyle DE\) oldal \(\displaystyle t\) felezőmerőlegesére, így elég belátni, hogy \(\displaystyle Q\) rajta van ezen a szimmetriatengelyen, mert akkor \(\displaystyle R\) is hasonlóképpen, így a két pont ugyanaz a pont.

Az \(\displaystyle AOQ\) háromszög egyenlő szárú, mert \(\displaystyle AO=AQ\) a négyzet oldala, szögeinek nagysága rendre \(\displaystyle 30^{\circ}\), \(\displaystyle 75^{\circ}\), \(\displaystyle 75^{\circ}\). Az \(\displaystyle OAB\) háromszög is egyenlő szárú, szögei ugyanígy \(\displaystyle 30^{\circ}\), \(\displaystyle 75^{\circ}\), \(\displaystyle 75^{\circ}\)-osak. A két egyenlő szárú háromszögnek közös szára az \(\displaystyle AO\), így egybevágó háromszögek. Ezért \(\displaystyle AB\) és \(\displaystyle OQ\) párhuzamosak. Így, mivel \(\displaystyle t\) párhuzamos \(\displaystyle AB\)-vel, így \(\displaystyle Q\) rajta van \(\displaystyle t\)-n. Ezzel az állítást beláttuk.

Statisztika:

A K/C. 882. feladat értékelése még nem fejeződött be.

A KöMaL 2025. decemberi matematika feladatai