 |
A P. 4848. feladat (2016. május) |
P. 4848. Egy hosszú lejtőn súrlódásmentesen mozoghat egy kiskocsi. A kocsit meglökjük a lejtésvonallal párhuzamosan valamekkora sebességgel, majd valamennyi idővel később hirtelen megállítjuk. Legfeljebb mennyi ideig tartott a kiskocsi mozgása, ha az utolsó másodpercben éppen feleakkora utat tett meg, mint a mozgásának teljes időtartama alatt?
Példatári feladat nyomán
(5 pont)
A beküldési határidő 2016. június 10-én LEJÁRT.
Megoldás. A leírt mozgás többféleképpen is megvalósulhat:
\(\displaystyle a)\) A kiskocsit a lejtőn lefelé lökjük meg.
\(\displaystyle b)\) A kiskocsit a lejtőn felfelé lökjük meg, és az végig felfelé mozog.
\(\displaystyle c)\) A felfelé meglökött kiskocsi megáll, majd még legalább 1 másodpercig mozog.
\(\displaystyle d)\) A felfelé indított kiskocsi sebessége a mozgás utolsó másodpercében csökken nullára és vált előjelet.
Ha valamekkora nagyságú gyorsulás mellett teljesül az időtartamokra vonatkozó feltétel, akkor a pillanatnyi sebességeket egy \(\displaystyle k\) számmal megszorozva továbbra is igaz marad az időarányokra vonatkozó feltétel; ebben az esetben azonban a gyorsulás nagysága a korábbi érték \(\displaystyle k\)-szorosa lesz. Mivel \(\displaystyle k\) tetszőleges, a végeredmény nem függhet az \(\displaystyle a\) gyorsulás nagyságától, az tehát akár \(\displaystyle 1~\rm m/s^2\)-nek is választható. (A továbbiakban SI mértékegységeket használunk, és azokat nem írjuk ki.)
Válasszuk a lejtőn lefelé mutató irányt pozitívnak, és ábrázoljuk a sebességet az idő függvényében! Jelöljük a mozgás teljes idejét \(\displaystyle T\)-vel, a test kezdősebességét pedig \(\displaystyle v_0\)-lal. A gyorsulás mindvégig \(\displaystyle a=+1\).
A felsorolt 4 esetben a sebesség-idő függvény az 1. ábrán látható grafikonokkal szemléltethető:
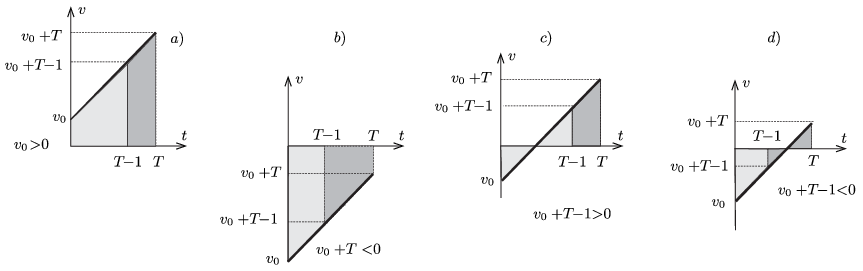
1. ábra
Az időtartamokra és utakra vonatkozó feltétel akkor teljesül, ha egy-egy ábrán a világosan és a sötéten jelölt terület nagysága megegyezik. Ez a feltétel kapcsolatot teremt \(\displaystyle T\) és \(\displaystyle v_0\) között, amiből leolvasható \(\displaystyle T\) lehetséges legnagyobb éretéke.
\(\displaystyle a)\) Ha a kiskocsit a lejtőn lefelé lökjük meg:
\(\displaystyle \left(v_0+\frac{T-1}{2}\right)(T-1)=v_0+T-\frac{1}{2},\)
ahonnan a kezdősebesség kifejezhető \(\displaystyle T\) segítségével:
\(\displaystyle v_0=\frac{2-(T-2)^2}{2(T-2)}.\)
Mivel \(\displaystyle v_0\ge0\) és \(\displaystyle T>1\), fenn kell álljon, hogy
\(\displaystyle 2<T\le 2+\sqrt2\approx 3{,}4.\)
A leghosszabb mozgás \(\displaystyle v_0=0\)-nak felel meg, ekkor \(\displaystyle T_\text{max}^{(a)}=3{,}4~\rm s.\)
\(\displaystyle b)\) Ha a kiskocsit a lejtőn felfelé lökjük meg, és az végig felfelé mozog:
A képletek ugyanazok, mint az előző esetben:
\(\displaystyle v_0=\frac{2-(T-2)^2}{2(T-2)},\)
de most \(\displaystyle v_0+T\le0\), ami akkor teljesül, ha
\(\displaystyle \sqrt2\le T<2.\)
A mozgás idejének felső határát (\(\displaystyle T_\text{max}^{(b)}=2{,}0~\rm s\)-ot) akkor közelíthetjük meg, ha a kezdősebesség abszolút értéke nagyon nagy.
\(\displaystyle c)\) A felfelé meglökött kiskocsi a mozgás utolsó másodpercében végig lefelé mozog:
\(\displaystyle \frac{v_0^2}{2}+ \frac{(v_0+T-1)^2}{2}=\frac{(v_0+T)^2}{2}-\frac{(v_0+T-1)^2}{2},\)
ahonnan algebrai átalakítások után kapjuk, hogy
\(\displaystyle v_0=\frac{2-T-\sqrt{T(4-T)}}{2}.\)
Látható, hogy teljesülnie kell a \(\displaystyle T\le 4\) feltételnek, és a határeset, \(\displaystyle T_\text{max}^{(c)}=4{,}0~\rm s\) megvalósulhat \(\displaystyle v_0=-1\) kezdősebesség esetén.
\(\displaystyle d)\) A felfelé meglökött kiskocsi a mozgás utolsó másodperc kezdetekor még felfelé, a végén pedig már lefelé mozog:
\(\displaystyle \frac{v_0^2}{2}- \frac{(v_0+T-1)^2}{2}=\frac{(v_0+T)^2}{2}+\frac{(v_0+T-1)^2}{2},\)
de teljesülnie kell még a \(\displaystyle 0\le v_0+T\le 1\) feltételnek is. Ebből \(\displaystyle \frac43\le T \le 2\) következik, vagyis \(\displaystyle T_\text{max}^{(d)}=2{,}0~\rm s.\) A \(\displaystyle T=2\) határesethez \(\displaystyle v_0=-1\) kezdősebesség tartozik. Ebben a mozgásformában a test 1 másodpercig mozog felfelé, majd ugyanennyi ideig lefelé.
Összefoglalva a vizsgálódást: A kiskocsit a lejtőn felfelé megfelelő sebességgel meglökve 1 másodperc alatt valamekkora \(\displaystyle s\) utat megtéve megáll, majd egyenletesen gyorsulva lefelé mozog tovább. A második másodpercben ugyancsak \(\displaystyle s\) utat tesz meg, a harmadikban \(\displaystyle 3s\), a negyedikben \(\displaystyle 5s\)-et. (Már Galilei is megfigyelte, hogy a lejtőn mozgó testek egymás utáni azonos időközökben megtett útjainak aránya az egymást követő páratlan számok arányával egyezik meg.) Mivel \(\displaystyle \tfrac12 (s+s+3s+5s) =5s\), a feladatban leírt feltétel teljesül, de ennél hosszabb idejű mozgással az nem valósítható meg.
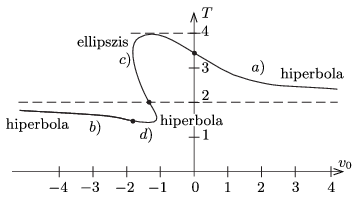
2. ábra
A 2. ábra mutatja a kezdősebesség és a mozgás ideje közötti meglehetősen összetett (hiperbola és ellipszis ívekből összetehető) kapcsolatot a különböző mozgásokra. Látható, hogy \(\displaystyle v_0\) nem határozza meg egyértelműen a mozgás teljes idejét, és \(\displaystyle T\)-hez sem rendelhető egyértelmű kezdősebesség. Az is leolvasható a grafikonról, hogy a mozgás teljes ideje alulról is korlátos, nem lehet kisebb, mint \(\displaystyle T_\text{min}=\tfrac43\) másodperc.
Statisztika:
24 dolgozat érkezett. 5 pontot kapott: Asztalos Bogdán, Balogh Menyhért, Bekes Nándor, Csorba Benjámin, Elek Péter, Fehér 169 Szilveszter, Fekete Balázs Attila, Kasza Bence, Szántó Benedek, Tomcsányi Gergely. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 7 versenyző.
A KöMaL 2016. májusi fizika feladatai
