 |
A P. 4964. feladat (2017. október) |
P. 4964. Legalább mekkora erővel lehet felborítani egy jégen csúszó jégkockát? (A súrlódás elhanyagolható.)
Példatári feladat
(5 pont)
A beküldési határidő 2017. november 10-én LEJÁRT.
Megoldás. Legyen a jégkocka oldaléle \(\displaystyle d\) hosszú, tömege \(\displaystyle m\) és hasson a jégkockára az egyik oldaléle középpontjában \(\displaystyle F\) nagyságú, a vízszintessel \(\displaystyle \alpha\) szöget bezáró erő (lásd az ábrát).
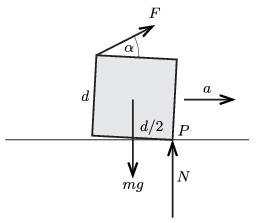
A felborulás határhelyzetében a kocka már egy kicsit megemelkedik, és csak a \(\displaystyle P\) ponton átmenő élénél érintkezik a vízszintes jégfelülettel. A kocka vízszintes irányban egyenletesen gyorsul, a függőleges gyorsulása és a forgási szöggyorsulása nulla. A mozgásegyenletek ennek megfelelően:
\(\displaystyle F\cos\alpha=ma,\)
\(\displaystyle F\sin\alpha+N-mg=0,\)
\(\displaystyle F\frac{d}{2}\cos\alpha+F\frac{d}{2}\sin\alpha-N\frac{d}{2}=0.\)
(A forgómozgás alapegyenletét a tömegközéppontra írtuk fel. Vigyázat: más pontra felírt forgási egyenlet rossz eredményre vezethet!)
A fenti egyenletekből az erőre az
\(\displaystyle F=\frac{1}{\cos\alpha+2\sin\alpha}mg\)
kifejezés adódik. Ennek legkisebb értéke a nevező maximumához tartozik. Belátható (egy 1 és 2 oldalélű, \(\displaystyle \alpha\) szögben megbillentett téglalap legmagasabb pontjának megkeresésével, vagy trigonometrikus átalakításokkal, esetleg differenciálszámítással), hogy
\(\displaystyle \cos\alpha+2\sin\alpha\le \sqrt{5},\)
és a szélsőérték \(\displaystyle \tg\alpha=2\), vagyis \(\displaystyle \alpha\approx63^\circ\) szöghöz tartozik.
A jégkockát tehát a súlyának \(\displaystyle 1/\sqrt{5}\) részével, annak kb. 45%-ával lehet felborítani.
Statisztika:
59 dolgozat érkezett. 5 pontot kapott: Bartók Imre, Csire Roland, Elek Péter, Fekete Balázs Attila, Guba Zoltán, Jánosik Áron, Kolontári Péter, Kozák András, Marozsák Tóbiás , Olosz Adél, Póta Balázs, Sal Dávid, Tófalusi Ádám. 4 pontot kapott: Békési Ábel, Fajszi Bulcsú, Marozsák Tádé, Molnár Mátyás, Ónodi Gergely. 3 pontot kapott: 16 versenyző. 2 pontot kapott: 15 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 4 versenyző. Nem versenyszerű: 4 dolgozat.
A KöMaL 2017. októberi fizika feladatai

