 |
A P. 5136. feladat (2019. május) |
P. 5136. \(\displaystyle A\) és \(\displaystyle B\) oldalú, téglalap alakú kép két felső sarkához egy fonál két végét rögzítjük, és egy szögre akasztjuk. Legalább milyen hosszú legyen a fonál, hogy a kép stabilan a szimmetrikus helyzetben maradjon? A szög és a fonál közötti súrlódás elhanyagolható, és a kép tömegközéppontja egybeesik a téglalap geometriai középpontjával.
Közli: Vigh Máté, Budapest
(5 pont)
A beküldési határidő 2019. június 11-én LEJÁRT.
Megoldás. Jelöljük a fonál hosszát \(\displaystyle L\)-lel, és legyen a fonál két vége a kép egyik, \(\displaystyle A\) hosszúságú oldalának \(\displaystyle F_1\) és \(\displaystyle F_2\) végpontjához rögzítve.
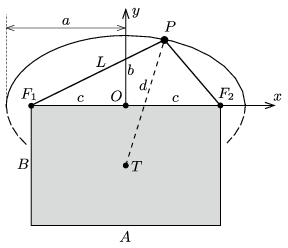
Adjuk meg a képtartó szög (az ábrán a \(\displaystyle P\) pont) helyét az \(\displaystyle F_1\) és \(\displaystyle F_2\) pontok \(\displaystyle O\) felezőpontján átmenő, a téglalap oldalaival párhuzamos tengelyű \(\displaystyle (x,y)\) derékszögű koordináta-rendszerben! A fonál hosszának állandóságából következik, hogy a \(\displaystyle P\) pont rajta fekszik az \(\displaystyle F_1\) és \(\displaystyle F_2\) fókuszpontú,
\(\displaystyle a=\frac{L}{2}, \qquad b=\frac{\sqrt{L^2-A^2}}{2} \)
féltengelyű ellipszisen. Az ellipszis egyenlete:
\(\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1,\)
vagyis
\(\displaystyle y=b\sqrt{1-\frac{x^2}{a^2}},\)
ami a kép méreteivel és a fonál hosszával kifejezve így írható:
\(\displaystyle y=\frac{\sqrt{L^2-A^2}}{2}\sqrt{1-\frac{4x^2}{L^2}}.\)
A szögre akasztott kép egyensúlyi helyzetben úgy helyezkedik el, hogy a \(\displaystyle P\)-re és \(\displaystyle T\)-re illeszkedő egyenes függőleges legyen. A kép helyzeti energiája a \(\displaystyle d=PT\) hossznak \(\displaystyle (-1)\)-szeresével arányos. Ha a szimmetrikus helyzetben (vagyis \(\displaystyle (x=0\)-nál) a \(\displaystyle d(x)\) függvénynek (és ezzel együtt \(\displaystyle d^2(x)\)-nek is) lokális maximuma van, akkor ez a helyzet stabil, ha viszont minimuma van, akkor az egyensúly labilis, a kép a legkisebb külső zavar hatására valamelyik oldalra kibillen.
Vizsgáljuk meg \(\displaystyle \left[d(x)\right]^2\) viselkedését a szimmetrikus helyzethez közeli (vagyis \(\displaystyle x\ll A\)-val jellemzett) tartományban:
\(\displaystyle \left[d(x)\right]^2=x^2+\left(y+\frac{B}{2}\right)^2=x^2+\left(b\sqrt{1-\frac{x^2}{a^2}}+\frac{B}{2}\right)^2.\)
Alkalmazva az \(\displaystyle \varepsilon\ll 1\) esetén érvényes
\(\displaystyle \sqrt{1+\varepsilon}\approx 1+\frac{\varepsilon}{2}\)
összefüggést, a vizsgált kifejezés közelítőleg így írható:
\(\displaystyle \left[d(x)\right]^2\approx x^2+\left(b -b\frac{x^2}{2a^2}+\frac{B}{2}\right)^2\approx \left(b+\frac{B}{2}\right)^2+ x^2 \left[1- \left(b+\frac{B}{2}\right)\frac{b}{a^2} \right].\)
A stabilitást a szögletes zárójelben álló kifejezés előjele dönti el. A kép helyzete stabil, ha
\(\displaystyle 1- \left(\frac{\sqrt{L^2-A^2}}{2} +\frac{B}{2}\right)\frac{2\sqrt{L^2-A^2}}{L^2} <0,\)
vagyis
\(\displaystyle 1<\frac{L^2-A^2}{L^2}+B\frac{\sqrt{L^2-A^2}}{L^2},\)
\(\displaystyle A^2<B\sqrt{L^2-A^2},\)
tehát
\(\displaystyle L>\frac{A}{B}\sqrt{A^2+B^2}.\)
Hasonlóan egyszerű a számolás, ha \(\displaystyle d^2\)-et \(\displaystyle y\)-nal fejezzük ki:
\(\displaystyle \left[d(y)\right]^2=a^2-a^2\frac{y^2}{b^2}+\left(y+\frac{B}{2}\right)^2,\)
de a \(\displaystyle 0<y<b\) feltételnek is teljesülnie kell. Ennek a másodfokú függvénynek \(\displaystyle y^*=\frac{b^2B}{2(a^2-b^2)}\)-nél van maximuma (parabolacsúcs). Ha ez az az érték \(\displaystyle b\)-nél kisebb, akkor ott van \(\displaystyle d^2\) maximuma, és a kép ferdén áll. Ha \(\displaystyle y^*\ge b\), akkor a tényleges maximum \(\displaystyle y=b\)-nél van, és a kép egyenesen áll. A
\(\displaystyle \frac{b^2B}{2(a^2-b^2)}\ge b\)
feltétel \(\displaystyle A\)-val és \(\displaystyle B\)-vel kifejezve:
\(\displaystyle L>\frac{A}{B}\sqrt{A^2+B^2}.\)
Statisztika:
9 dolgozat érkezett. 5 pontot kapott: Elek Péter, Markó Gábor, Marozsák Tádé, Olosz Adél, Tiefenbeck Flórián. 4 pontot kapott: Lipták Gergő. 2 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2019. májusi fizika feladatai

