A P. 5457. feladat (2023. január)

P. 5457. Hőszigetelt, hengeres tartály belső hossza \(\displaystyle L\). A tartályt egy hőszigetelő dugattyú két részre osztja; a bal oldali térfélben egyatomos ideális gáz, a jobb oldaliban vákuum van (lásd az ábrát). A dugattyút a tartály jobb oldali végével rugó köti össze, melynek feszítetlen hossza \(\displaystyle L\). A gázt a bal oldali térfélben lévő fűtőszál segítségével lassan melegíteni kezdjük.

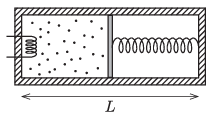
Határozzuk meg a gáz mólhőjét ebben a folyamatban!

Oroszországi feladat nyomán

(5 pont)

A beküldési határidő 2023. február 15-én LEJÁRT.

Megoldás. A rugó összenyomódása (tehát az általa kifejtett erő és az annak megfelelő nyomás) a bal oldali térfélben lévő gáz térfogatával arányos: \(\displaystyle p=\lambda V\), ahol \(\displaystyle \lambda\) állandó (ez azért igaz, mert a rugó nyújtatlan hossza megegyezik a tartály belső hosszával).

Az egyatomos gáz belső energiája:

\(\displaystyle E=\frac32 pV=\frac32\lambda V^2,\)

aminek megváltozása a térfogat kicsiny \(\displaystyle \Delta V\) változásakor:

\(\displaystyle \Delta E=\frac32\lambda \left[(V+\Delta V)^2-V^2 \right]\approx 3\lambda V \Delta V.\)

A tágulás során a gáz által végzett munka:

\(\displaystyle W'=p\Delta V=\lambda V \Delta V.\)

A hőtan I. főtétele szerint

\(\displaystyle Q=\Delta E+W'= 4\lambda V \Delta V.\)

Másrészt a gáztörvény alapján

\(\displaystyle pV=\lambda V^2=nRT,\)

ami a kicsiny megváltozásokra ezt adja:

\(\displaystyle nR(T+\Delta T)=\lambda (V+\Delta V)^2,\)

vagyis

\(\displaystyle nRT+nR\Delta T=\lambda V^2+2\lambda V\Delta V+\lambda(\Delta V)^2,\)

amiből

\(\displaystyle nR\Delta T= 2\lambda V \Delta V+\lambda(\Delta V)^2\approx 2\lambda V \Delta V.\)

A gáz mólhője erre a folyamatra:

\(\displaystyle C=\cfrac{Q}{n\Delta T}=2R.\)

Statisztika:

45 dolgozat érkezett.
5 pontot kapott:	Arnold Lőrinc, Beke Bálint, Beke Botond, Bocor Gergely, Bodré Zalán, Bogdán Benedek, Bunford Luca, Chrobák Gergő, Csiszár András, Dercsényi Bence, Fehérvári Donát, Flóring Balázs, Fórizs Borbála, Halász Henrik, Katona Attila Zoltán, Kis Márton Tamás, Klement Tamás, Kovács Barnabás, Kovács Kristóf , Márfai Dóra, Masa Barnabás, Merics Vilmos, Molnár Kristóf, Nemeskéri Dániel, Schmercz Blanka, Seprődi Barnabás Bendegúz, Szabó Márton, Szabó Zsombor.
4 pontot kapott:	Bencz Benedek, Osváth Emese, Tárnok Ede .
3 pontot kapott:	4 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2023. januári fizika feladatai