A KöMaL 2021. áprilisi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2021. május 17-én LEJÁRT. |
I. 535. Lőrinc nagyon kedveli a pozitív egész számokat. Most kitalált egy pozitív egészekből álló növekvő számsorozatot, amit számláncnak nevezett el. A lánc egy tetszőlegesen választott pozitív egésszel kezdődik, ez a lánc első száma. Minden további számot az őt megelőző számból készítünk. A lánc tetszőleges \(\displaystyle n\)-edik számára igaz, hogy ő és a rákövetkező szám legnagyobb közös osztója az \(\displaystyle n\)-edik prímszám. Ha több ilyen szám is van, akkor a láncba azok közül a legkisebbet tesszük bele. Ha nincs megfelelő szám, akkor a lánc megszakad.
Lőrinc kiszámolt néhány láncot különböző számokkal indulva, de úgy látta, hogy a láncok nagyon rövidek, csak legföljebb négy hosszú láncot talált. Ilyen volt például a 160, 162, 165, 170. Szerette volna tudni, hogy melyek azok a legföljebb háromjegyű számok, amelyeket első számnak választva a lánc legalább öt hosszú.
Készítsünk programot, amely megadja Lőrinc kérdésére a választ, tehát a legalább öt hosszú, 1000-nél kisebb egésszel induló láncokat.
A standard kimenet minden sorában egy-egy olyan lánc szerepeljen, amely a leghosszabbak az 1000-nél kisebb számmal kezdődő láncok között.
Beküldendő egy tömörített i535.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
I. 536. (É). Az autóversenyzés a technikai sportok közé tartozik. Van olyan ága, ahol nem lehet minden autó a versenypályán, kevés az előzési lehetőség, ezért egyenként indítják a versenyzőket. Ebben az esetben az utolért versenyzőnek utat kell adnia a mögötte érkező gyorsabbnak.
Egy ilyen autóverseny adatai állnak rendelkezésre az autoforras.txt tabulátorral tagolt, UTF-8 kódolású állományban.
A versenyen 36-an indultak, róluk a következő adatokat tudjuk (az adatok indítási sorrendben vannak): az autók azonosítója, a rajtolás és a célba érkezés időpontja másodperc pontossággal.
Táblázatkezelő program segítségével oldjuk meg a következő feladatokat.
A megoldás során vegyük figyelembe a következőket:
\(\displaystyle \bullet\) Segédszámításokat a K oszloptól jobbra végezhetünk.
\(\displaystyle \bullet\) Amennyiben lehetséges, a megoldás során képletet, függvényt, hivatkozást használjunk, hogy az alapadatok módosítása esetén is a kívánt eredményeket kapjuk.
1. Töltsük be az autoforras.txt szövegfájlt a táblázatkezelőbe az A1-es cellától kezdődően. Munkánkat i536 néven mentsük el a táblázatkezelő alapértelmezett formátumában.
2. Hozzuk létre a munkalapon a minta szerinti cellákban a hiányzó szövegeket, feliratokat, amelyek a további munkát segítik.
3. A D oszlop celláiban számítsuk ki az autók versenyidejét. Ha a versenyző nem ment végig a pályán, mert például műszaki hibája volt, vagy a versenybírók kizárták, akkor a nem fejezte be felirat jelenjen meg.
4. Az I5-ös cellában írassuk ki, hogy hány versenyző nem fejezte be a versenyt.
5. Az E oszlop celláiban adjuk meg, hogy a versenyzők a célba érkezéskor, az addig beérkezettek eredmények ismeretében, hányadik helyen álltak. A versenyt nem befejezők mindannyian az utolsó sorszámot kapják.
6. Az I2-es cellában adjuk meg, hogy hány versenyző kaphatta azt az információt a csapatától a saját célba érkezésekor, hogy az első háromban van.
7. Az F oszlop celláiban határozzuk meg, hogy a verseny befejeztével ki hányadik helyezést ért el. Azonos versenyidők esetén (holtverseny) a versenyzők azonos helyezésűek és a következő helyezési sorszámot nem adják ki. Például három azonosan eredménnyel negyedik helyezést elért versenyző után a következő versenyző a hetedik helyezett.
8. Az I10:J19-es cellákban függvények segítségével adjuk meg a helyezési lista első tíz versenyzőjének azonosítóját és helyezését. Azonos helyezésű versenyzők lehetnek.
9. Az A oszlop celláiban jelenítsük meg félkövér betűstílussal azoknak az autóknak az azonosítóját, akiknek az eredmények alapján biztosan előznie kellett a pályán. Alkalmazzunk feltételes formázást, hogy más eredmények esetén is helyes formázást kapjunk.
10. Az A:F cellatartományban az első három helyezett sorának celláiban a cellakitöltést az érem színének megfelelően, feltételes formázással adjuk meg: arany RGB(255,215,0), ezüst RGB(192,192,192), bronz RGB(204,153,102).
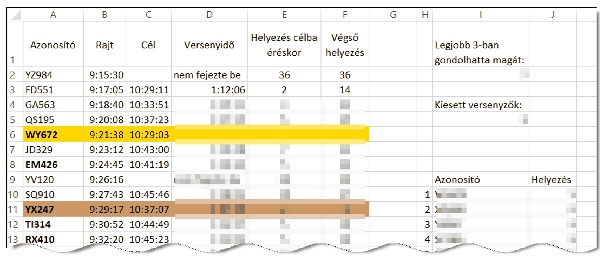
11. A munkalap celláiban az igazítást a mintának megfelelően készítsük el.
Beküldendő egy tömörített i536.zip állományban a munkafüzet, valamint egy rövid dokumentáció, amelyből kiderül az alkalmazott táblázatkezelő neve és verziószáma.
Letölthető állomány: autoforras.txt
(10 pont)
I. 537. A táblázatkezelők újabb és újabb verzióiban egyre több gyári függvény segíti a felhasználók munkáját. Némi kreativitással praktikusan használhatjuk munkánkhoz, feladatainkhoz. Ennek a kreativitásnak a kiaknázásáról szól ez a feladat.
Hozzuk létre a táblázatkezelőben az i537 nevű munkafüzetet, annak függvény névre átnevezett egyetlen munkalapjára a mintán látható cellákban sárga háttérrel szereplő alapadatokat gépeljük be, és formázzuk a minta szerint.
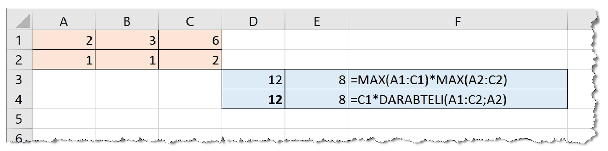
A D oszlopba a D3 cellától kezdve lefelé írjunk olyan – függvényeket is tartalmazó – képleteket, amelyek eredménye a mintán látható 12 érték. A felhasznált képletekben és a függvények argumentumaiban csak az A1:C2 tartomány cellái szerepelhetnek (nem feltétlenül az összes), más cellahivatkozások és konstansok nem. Nem számít függvényhasználatnak, ha az eredmény az adott függvény nélkül is ugyanaz az érték, tehát ha egy egész értéket adó, függvény nélküli képlet eredményét függvénnyel kerekítjük.
Nézzünk meg néhány példát:
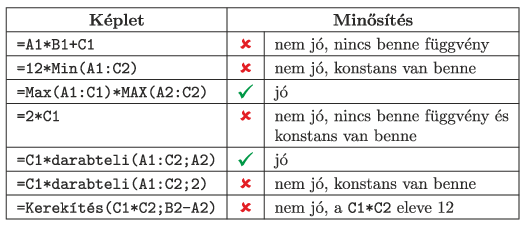
A feladat: Keressünk a D oszlopba minél több lényegesen eltérő, a feltételeknek megfelelő függvényt. Nem lényegesen eltérőek az alábbi párok:
Max(A1:C1)*MAX(A2:C2) és Max(A2:C2)*MAX(A1:C1)
Max(A1:C1)*MAX(A2:C2) és Max(B1:C1)*MAX(B2:C2)
C1*darabteli(A1:C2;A2) és C1*darabteli(A1:C2;B2)
Az E oszlopban jelenjen meg a D oszlopban megjelenő képlet eredménye úgy, mintha a C1 cella értéke 4 lenne. Az F oszlopban jelenjen meg a D oszlop ugyanezen sorában szereplő képlet szövege.
A D, E és F oszlop nem üres cellái kapják meg a mintán a D3 cellában látható formázást (szegélyezett halványkék hátterű).
Minden, a feltételeknek megfelelő sorért 0,2 pont kapható, de az összes pontszám nem haladhatja meg a 10 pontot. A fenti jó példák felsorolásáért sem jár pont.
A feladatban nem használható saját függvény vagy makró.
Beküldendő egy i537.zip tömörített mappában a táblázatkezelő munkafüzet és egy rövid dokumentáció, amelyben szerepel a megoldáshoz alkalmazott táblázatkezelő neve, verziószáma.
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2021. május 17-én LEJÁRT. |
I/S. 53. Adott egy \(\displaystyle N\) hosszú bitsorozat. Az \(\displaystyle i\)-edik bitet \(\displaystyle B[i]\)-vel jelöljük. Minden lehetséges \(\displaystyle 1\le x\le y\le N\)-re a bitsorozat \(\displaystyle x\)-edik elemétől az \(\displaystyle y\)-adik eleméig terjedő részét kiegyensúlyozottnak nevezzük, ha ugyanannyi 1-es értékű bitet tartalmaz, mint 0-s értékűt (tehát ha a \(\displaystyle B[x]\), \(\displaystyle B[x+1]\), ..., \(\displaystyle B[y]\) bitek közt azonos számú az 1-es és a 0-s értékű).
Adjuk meg, hogy hány olyan \(\displaystyle x\), \(\displaystyle y\) páros van, amire kiegyensúlyozott részt kapunk.
Bemenet: az első sor tartalmazza az \(\displaystyle N\) számot, a második az \(\displaystyle N\) hosszú bitsorozatot.
A kimenet egyetlen sorában adjuk meg, hogy hány kiegyensúlyozott rész van.
| Bemenet (a / jel sortörést jelent) | Kimenet |
| 5 /10101 | 6 |
A keresett \(\displaystyle x\), \(\displaystyle y\) párosok: \(\displaystyle (1,2)\), \(\displaystyle (2,3)\), \(\displaystyle (3,4)\), \(\displaystyle (4,5)\), \(\displaystyle (1,4)\), \(\displaystyle (2,5)\).
Korlátok: \(\displaystyle 1\le N\le {10}^{5}\).
Értékelés: a pontok 50%-a kapható, ha \(\displaystyle N\le 1000\).
Beküldendő egy is53.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2021. május 17-én LEJÁRT. |
S. 152. A LONG teniszbajnokságra \(\displaystyle 2N-1\) versenyző nevezett. Közülük kell kiválasztani a legjobb \(\displaystyle N\) játékost, akik díjat kapnak. A sok nevezőre való tekintettel nem szeretnének mindenkit egyszerre versenyeztetni, ezért a versenyt több napon keresztül bonyolítják le. A versenyzők egy várólistára kerülnek, és hogy melyik nap és kivel játszanak meccset, azt a következők szerint határozzák meg.
Az első nap a várólista első \(\displaystyle N\) versenyzője versenyez egymással egyenes kiesésben, azaz, ha valaki veszít, aznap már nem játszhat. Ők megkapják az \(\displaystyle 1,2,\ldots, N\) sorszámokat. Egy nap több körből áll, és egyszerre csak egy meccset játszanak. Mindig az a két játékos játssza a következő meccset, akik még nem játszottak az adott körben és a sorszámuk a legkisebb. (Első a másodikkal, harmadik a negyedikkel stb. ebben a sorrendben.) Minden kör végén, ha valaki partner nélkül marad, akkor továbbjut a következő körbe. Ezt addig csinálják, amíg már csak egy versenyző marad, ő lesz a nap győztese.
Egy mérkőzés győztese az a versenyző, aki ,,több trükköt ismer''. Egyenlőség esetén a mérkőzés aznapi sorszáma dönt. Ha ez páratlan, akkor a kisebb sorszámú versenyző nyer, ha páros, akkor a nagyobb sorszámú.
Minden nap végén kiosztják a díjakat. Elsőként a nap győztese kap díjat, majd azok a versenyzők, akiket a győztes ejtett ki, a kiesés szerinti fordított sorrendben egy-egy pontot kapnak. (A pontok a napok során összeadódnak.) Ha valaki így összegyűjt két pontot, és még nincs meg az \(\displaystyle N\) számú díjazott, akkor ő is díjazottá válik.
Ha még nincs meg az \(\displaystyle N\) számú díjazott, akkor újabb nap következik. Ezen a napon szintén \(\displaystyle N\) versenyző játszik. Az előző napon díjazottak helyére a díjazás sorrendjében bekerülnek a várólistáról a következő olyan játékosok, akik még nem versenyeztek. Ha például a hármas sorszámú versenyző nyert, és az előző napon még a kettes és ötös is díjat kapott ebben a sorrendben, akkor a következő három versenyző a várólistáról a hármas, kettes és ötös sorszámmal versenyez ezen a napon.
Bemenet: az első sor az \(\displaystyle N\) számot tartalmazza. A második sor \(\displaystyle 2N-1\) pozitív számot tartalmaz. Az \(\displaystyle i\)-edik szám a várólistán \(\displaystyle i\)-edik versenyző által ismert trükkök számát adja meg.
Kimenet: a kimenet \(\displaystyle i\)-edik sora az \(\displaystyle i\)-edik napon díjazottak számát, majd a díjazott(ak) sorszámát tartalmazza a díjazás sorrendjében.
Példa:
| Bemenet | Kimenet (a / jel sortörést helyettesít) |
| 5 / 4 3 2 4 1 2 5 1 4 | 1 1 / 3 4 5 2 / 1 4 |
Magyarázat: az első nap mérkőzései \(\displaystyle \text{mérkőzés sorszáma} : \text{győztes} -\text{vesztes}\) formátumban: \(\displaystyle 1:1-2\), \(\displaystyle 2:4-3\), \(\displaystyle 3:1-4\), \(\displaystyle 4:1-5\), győztes: 1., pontot kap: \(\displaystyle 5,4,2\). Új játékos 2 trükkel az 1. sorszámú helyre. A második nap: \(\displaystyle 1:2-1\), \(\displaystyle 2:4-3\), \(\displaystyle 3:4-2\), \(\displaystyle 4:4-5\), győztes: 4., pontot kap: \(\displaystyle 5,2,3\). Új játékosok \(\displaystyle 5,1,4\) trükkökkel a \(\displaystyle 4,5,2\) helyekre. A harmadik nap: \(\displaystyle 1:2-1\), \(\displaystyle 2:4-3\), \(\displaystyle 3:4-2\), \(\displaystyle 4:4-5\), győztes: 4., pontot kap: \(\displaystyle 5,2,3\). A 3. sorszámú versenyző már nem kap díjat, mert megvan az \(\displaystyle N\) díjazott.
Korlátok: \(\displaystyle 1\le N\le 32\,768\), \(\displaystyle 1\le \text{ismert trükkök száma}\le 1024\). Időkorlát: 1 mp.
Értékelés: A pontok 50%-a kapható, ha \(\displaystyle N< 100\).
Beküldendő egy s152.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.
