A KöMaL 2021. decemberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2022. január 10-én LEJÁRT. |
K. 709. Egy család egy egzotikus hagymafajtát termeszt saját fogyasztásra. A hagymából minden évben 400 darabot szeretnének megenni. A hagyma magról kel ki, melyet minden évben a növényen is meg tudunk termelni. Minden egyes hagymanövény 51 magot tud hozni, de ha már ,,felmagzott'', akkor az a része, melyet a család ,,hagymaként'' elfogyasztana, elsorvad, mert a benne levő anyagokat a magok növekedésére fordítja. Minimálisan hány magot kell az első évben beszerezni, ha azokból az adott évre kívánt mennyiségű hagymát, továbbá annyi magot szeretnének kitermelni, hogy a továbbiakban már sose kelljen magot vásárolni?
(5 pont)
K. 710. Néhány dodekaédert és néhány ikozaédert tettünk az asztalra. A testeknek összesen 792 csúcsuk és 936 lapjuk van. Hány dodekaéder és hány ikozaéder van az asztalon?
(5 pont)
K. 711. Andi kedvenc száma a 2468. Bandi kedvenc száma is négyjegyű és tudjuk, hogy pontosan két olyan számjegye van, ami megegyezik Andi kedvenc számának két számjegyével, ráadásul a megegyező számjegyek ugyanazon a helyi értéken vannak a két számban. Hány olyan négyjegyű pozitív egész szám van, ami ezek alapján Bandi kedvenc száma lehetne?
(5 pont)
 |
K/C-jelű feladatokA beküldési határidő 2022. január 10-én LEJÁRT. |
K/C. 712. Egymás mellé helyezünk 2022 db négyzet alakú falapot, majd 2021 db korongra felírjuk az egész számokat 1-től 2021-ig. A korongokat tetszőleges sorrendben elhelyezzük a falapokon úgy, hogy a jobb szélső négyzetre nem helyezünk korongot (minden falapra egy korong kerül). Ezek után egy lépésben egy tetszőleges korongot áthelyezhetünk az éppen üresen álló fanégyzetre. A célunk az, hogy a korongokon álló számok balról jobbra haladva növekvő sorrendben legyenek, és a jobb szélső négyzet üres legyen. Maximálisan hány lépésre van ehhez szükségünk? Mutassunk is olyan kezdeti elrendezést, amely az általunk megállapított maximális lépésszámot igényli a sorba rendezéshez.
(5 pont)
K/C. 713. Egy 6 cm oldalhosszúságú négyzet oldalaira – mint átmérőkre – egy-egy kört rajzoltunk, majd a négyzet középpontja körül megszerkesztettük azt a kört, melynek a sugara a négyzet oldalával egyenlő. Három síkrészt jelöltünk az ábrán (I., II., III.). Számítsuk ki az I., II. és III. részek területét.
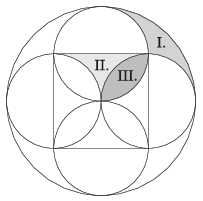
(5 pont)
 |
C-jelű feladatokA beküldési határidő 2022. január 10-én LEJÁRT. |
C. 1694. Határozzuk meg az alábbi egyenlet megoldását a valós számok halmazán:
$$\begin{gather*} x-2021-\frac{x-2020}{2}+\frac{x-2019}{3}-\frac{x-2018}{4}+\frac{x-2017}{5}-\ldots +{}\\ {} + \frac{x-3}{2019}-\frac{x-2}{2020}+\frac{x-1}{2021}-\frac{x}{2022}=0. \end{gather*}$$Javasolta: Sáfár Lajos (Ráckeve)
(5 pont)
C. 1695. Egy körvonalhoz rá merőlegesen hozzárögzítünk egy sugárnyi \(\displaystyle (R)\) hosszúságú szakaszt (lásd az ábrát). Belefér-e két, ilyen szakasszal ellátott kör (,,serpenyő'') egy olyan téglalapba, aminek az egyik oldala a kör átmérője (\(\displaystyle 2R\)), a másik pedig kétszer akkora (\(\displaystyle 4R\))? Az alakzatok és a téglalap érinthetik, de nem metszhetik és nem fedhetik egymást.

Javasolta: Gáspár Merse Előd (Budapest)
(5 pont)
C. 1696. Adottak az \(\displaystyle a\) és a \(\displaystyle b\) párhuzamos egyenesek, melyeken kijelölünk rendre \(\displaystyle 10\), illetve \(\displaystyle 15\) darab pontot. Tekintsük az összes olyan szakaszt, melynek egyik végpontja az \(\displaystyle a\), másik pedig a \(\displaystyle b\) egyenes kijelölt pontjai közül való. Legfeljebb hány metszéspontja lehet összesen ezeknek a szakaszoknak?
(5 pont)
C. 1697. Az \(\displaystyle ABC\) szabályos háromszögben a \(\displaystyle BC\), \(\displaystyle CA\), \(\displaystyle AB\) oldalakon rendre kijelöltük a \(\displaystyle D\), \(\displaystyle E\), \(\displaystyle F\) belső pontokat úgy, hogy \(\displaystyle DEF\) szabályos háromszög legyen. Ezután a \(\displaystyle BC\) és \(\displaystyle AC\) oldalakra kifelé a \(\displaystyle BDA'\) és \(\displaystyle AEB'\) szabályos háromszögeket rajzoltuk. Bizonyítsuk be, hogy az \(\displaystyle AB\) oldalon van olyan pont, amelyből az \(\displaystyle A'E\) és \(\displaystyle B'D\) szakaszok mindegyike derékszögben látszik.
(5 pont)
C. 1698. Zoli nem szereti a könyveket, ám elhatározza, hogy ennek ellenére összesen pontosan 2021 oldalt fog elolvasni a 2021. évben, egymást követő napokon. Úgy tervezi, hogy minden nap egy oldallal többet olvas, mint az előző napon. Hány oldalt olvasson első napon, ha tudjuk, hogy Zoli a lehető legtöbb napra szeretné elnyújtani a 2021 oldal elolvasását, ám időhiány miatt nem tud 100 oldalnál többet olvasni egy nap?
Javasolta: Sáfár Lajos (Ráckeve)
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2022. január 10-én LEJÁRT. |
B. 5206. Egy \(\displaystyle n\)-jegyű \(\displaystyle \overline{a_1a_2a_3\ldots a_n}\) számot hegyszerűnek nevezünk, ha van olyan \(\displaystyle 1 \le k \le n\) egész, amelyre \(\displaystyle a_1,a_2,\ldots,a_k\) szigorúan monoton növekvő, míg \(\displaystyle a_k,a_{k+1},\ldots,a_n\) szigorúan monoton csökkenő sorozat. (Például az 1, 121, 1231 számok hegyszerűek, de az 1442 és az 12313 nem hegyszerűek.) Hány hegyszerű szám van?
(3 pont)
B. 5207. Bizonyítsuk be, hogy minden \(\displaystyle n\ge 2\) természetes számra léteznek olyan \(\displaystyle 2\le x_1<x_2<x_3<\ldots<x_n\) pozitív egész számok, amelyekre
\(\displaystyle x_1!\cdot x_2!\cdot x_3!\cdot \ldots \cdot x_n! \)
négyzetszám.
Javasolta: Szoldatics József (Budapest)
(4 pont)
B. 5208. Egy kör \(\displaystyle AB\) és \(\displaystyle CD\) húrjai merőlegesek egymásra, a húrok egyenesei a körön kívüli \(\displaystyle P\) pontban metszik egymást; a \(\displaystyle P\)-ből a körhöz húzott érintőszakasz hossza \(\displaystyle e\). Mutassuk meg, hogy az \(\displaystyle AD\) és \(\displaystyle BC\) szakaszok hosszainak mértani közepe legalább \(\displaystyle \sqrt2\, e\).
Javasolta: Kocsis Szilveszter (Budapest)
(4 pont)
B. 5209. Egy \(\displaystyle 2022\) elemű, egészekből álló halmaznak legfeljebb hány olyan kételemű részhalmaza lehet, melyre a két elem összege szintén a halmazhoz tartozik?
(5 pont)
B. 5210. A \(\displaystyle \mathcal{P}_1\), \(\displaystyle \mathcal{P}_2\) és \(\displaystyle \mathcal{P}_3\) parabolák fókuszpontja közös, bármely kettő közülük pontosan kettő pontban metszi egymást. A \(\displaystyle \mathcal{P}_i\) és \(\displaystyle \mathcal{P}_j\) parabolák két metszéspontjára illeszkedő egyenest jelölje \(\displaystyle e_{ij}\). Mutassuk meg, hogy az \(\displaystyle e_{12}\), \(\displaystyle e_{13}\) és \(\displaystyle e_{23}\) egyenesek illeszkednek egy közös pontra.
(5 pont)
B. 5211. Oldjuk meg a pozitív egész számok halmazán a következő egyenletet:
\(\displaystyle 5^x-2^y=1. \)
(5 pont)
B. 5212. Igazoljuk, hogy létezik olyan pozitív egész szám, amely legalább 2021-féleképpen állítható elő úgy, hogy egy (tízes számrendszerben felírt) pozitív egész számhoz hozzáadjuk a számjegyeinek összegét.
Javasolta: Sándor Csaba (Budapest)
(6 pont)
B. 5213. Igazoljuk, hogy ha \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) pozitív valós számok, akkor
\(\displaystyle c\sqrt{a^2+b^2-ab}+a\sqrt{b^2+c^2-bc}\ge b\sqrt{c^2+a^2+ca}\,. \)
Milyen esetben teljesül az egyenlőség?
Javasolta: Schultz János (Szeged)
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2022. január 10-én LEJÁRT. |
A. 812. Két játékos a következő játékot játssza: van két kupac, melyekből felváltva kell kavicsokat elvenniük, és az nyer, aki az utolsó kavicsot elveszi. Ha a kupacok mérete egy adott pillanatban \(\displaystyle A\) és \(\displaystyle B\), akkor a soron következő játékos valamelyik kupacból elveheti \(\displaystyle A\) egy többszörösét vagy \(\displaystyle B\) egy többszörösét.
Határozzuk meg azokat az \(\displaystyle (k,n)\) számpárokat, melyekre a második játékosnak van nyerő stratégiája, ha kezdetben az egyik kupacban \(\displaystyle k\), a másikban pedig \(\displaystyle n\) darab kavics van.
Javasolta: Pálvölgyi Dömötör (Budapest)
(7 pont)
A. 813. Legyen \(\displaystyle p\) prímszám és \(\displaystyle k\) pozitív egész. Legyen továbbá
\(\displaystyle t=\sum_{j=0}^{\infty} \left\lfloor\frac{k}{p^j}\right\rfloor. \)
\(\displaystyle a)\) Legyen \(\displaystyle f(x)\) egy egész együtthatós, \(\displaystyle 1\) főegyütthatós, \(\displaystyle k\)-adfokú polinom, amelynek a konstans tagját osztja \(\displaystyle p\). Bizonyítsuk be, hogy létezik \(\displaystyle n\in \mathbb{N}\), amelyre \(\displaystyle p\mid f(n)\), de \(\displaystyle p^{t+1}\nmid f(n)\).
\(\displaystyle b)\) Bizonyítsuk be, hogy a fenti állítás éles, azaz létezik olyan egész együtthatós, \(\displaystyle 1\) főegyütthatós, \(\displaystyle k\)-adfokú \(\displaystyle g(x)\) polinom, amelynek a konstans tagját osztja \(\displaystyle p\), és ha egy \(\displaystyle n\in \mathbb{N}\) esetén \(\displaystyle p\mid g(n)\) teljesül, akkor \(\displaystyle p^t\mid g(n)\) is igaz.
Javasolta: Szabó Kristóf (Budapest)
(7 pont)
A. 814. Adott a síkon 666 különböző pont úgy, hogy nem fedhetők le 10 darab egyenessel. Bizonyítandó, hogy ekkor kiválasztható közülük 66 pont úgy, hogy már azok sem fedhetők le 10 darab egyenessel.
Javasolta: Hujter Mihály (Budapest)
(7 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
