A KöMaL 2022. novemberi matematika feladatai

K-jelű feladatok A beküldési határidő 2022. december 12-én LEJÁRT.

---

K. 739. Fülöp a következő megfigyeléseket tette az ősz egy időszakában:

1. A megfigyelt idő alatt 11 napon esett az eső.

2. Esős délelőttöt mindig napos délután követett.

3. Összesen 9 délelőtt és 12 délután volt napos idő.

Hány napon nem esett egyáltalán?

(5 pont)

megoldás, statisztika

---

K. 740. Egy \(\displaystyle 3\times12\)-es téglalapot szeretnénk lefedni 12 db \(\displaystyle 1\times3\)-as téglalappal. Hányféleképpen tehetjük ezt meg?

(5 pont)

megoldás, statisztika

---

K. 741. Induljunk ki az \(\displaystyle 1, 2, 3, 4, 5, 6, 7, 8, 9\) számokból. Egy lépésben kiválaszthatunk két számot, amelyeket 1-gyel megnövelünk. El lehet-e néhány lépésben érni, hogy mindegyik szám a 10-es legyen?

(5 pont)

megoldás, statisztika

K/C-jelű feladatok A beküldési határidő 2022. december 12-én LEJÁRT.

---

K/C. 742. Dani most tanulja az angol ábécét, és el is mondta az első nyolc betűjét (A, B, C, D, E, F, G, H), csak némileg rossz sorrendben. A nyolc betűből csak ötöt mondott jól (annyiadik betűként, ahányadik az ABC-ben). Hány ilyen különböző sorrendje van ennek a nyolc betűnek?

(5 pont)

megoldás, statisztika

---

K/C. 743. Az \(\displaystyle ABCD\) téglalap \(\displaystyle BC\) oldalának felezőpontja \(\displaystyle E\), \(\displaystyle CD\) oldalának \(\displaystyle D\)-hez közelebbi harmadolópontja \(\displaystyle F\). Az \(\displaystyle AE\) szakasz felezőpontja \(\displaystyle G\), az \(\displaystyle EF\) szakasz \(\displaystyle E\)-hez közelebbi harmadolópontja pedig \(\displaystyle H\). Hányadrésze az \(\displaystyle FGH\) háromszög területe az \(\displaystyle ABCD\) téglalap területének?

(5 pont)

megoldás, statisztika

C-jelű feladatok A beküldési határidő 2022. december 12-én LEJÁRT.

---

C. 1738. Egy természetes számot nevezzünk kiegyensúlyozottnak, ha tízes számrendszerben felírva éppen annyi számjegye van, ahány különböző prímosztóval rendelkezik. Például a \(\displaystyle 21\) kiegyensúlyozott, de a \(\displaystyle 42\) nem. Igaz-e, hogy végtelen sok kiegyensúlyozott szám van?

Javasolta: Kozma Katalin Abigél (Győr)

(5 pont)

megoldás, statisztika

---

C. 1739. A valós számok halmazának lehető legbővebb részhalmazán értelmezzük a következő függvényeket: \(\displaystyle f(x)=\sqrt{x+5}\,\), \(\displaystyle g(x)=\frac{-2x+8}{5}\) és \(\displaystyle h(x)=[x+3]\). Határozzuk meg a három függvénygrafikon közös pontjainak koordinátáit (\(\displaystyle [a]\) az \(\displaystyle a\) valós szám egészrészét jelenti, vagyis azt a legnagyobb egész számot, amely nem nagyobb \(\displaystyle a\)-nál).

Javasolta: Bíró Bálint (Eger)

(5 pont)

megoldás, statisztika

---

C. 1740. Az \(\displaystyle ABCD\) paralelogramma \(\displaystyle CD\) oldalán felvesszük a \(\displaystyle P\) belső pontot, a \(\displaystyle CD\)-vel párhuzamos \(\displaystyle AB\) oldalon a \(\displaystyle Q\) belső pontot. A \(\displaystyle PA\) és \(\displaystyle QD\) szakaszok metszéspontja \(\displaystyle M\), a \(\displaystyle PB\) és \(\displaystyle QC\) szakaszok metszéspontja \(\displaystyle N\).

Tegyük fel, hogy \(\displaystyle MN\nparallel{AB}\), és \(\displaystyle MN\) a \(\displaystyle CD\) egyenesét az \(\displaystyle X\), \(\displaystyle AB\) egyenesét az \(\displaystyle Y\) pontban metszi. Bizonyítsuk be, hogy \(\displaystyle DX=BY\).

(Amerikai versenyfeladat)

(5 pont)

megoldás, statisztika

---

C. 1741. Az \(\displaystyle ABCD\) konvex négyszög \(\displaystyle AC\) és \(\displaystyle BD\) átlóinak metszéspontja \(\displaystyle M\). Lehetséges-e, hogy az \(\displaystyle ABM\), \(\displaystyle BCM\), \(\displaystyle CDM\), \(\displaystyle DAM\) háromszögek területe ebben a sorrendben egy

\(\displaystyle a)\) nemkonstans számtani sorozat,

\(\displaystyle b)\) nemkonstans mértani sorozat
közvetlen egymás utáni négy tagja?

Javasolta: Bíró Bálint (Eger)

(5 pont)

megoldás, statisztika

---

C. 1742. Tekintsük a következő (a valós számok halmazának lehető legbővebb részhalmazán értelmezett) függvényeket:

\(\displaystyle f_0(x)=\frac{1}{1-x}, \quad\text{valamint}\quad f_n(x)=f_0\big(f_{n-1}(x)\big), \)

minden \(\displaystyle n\) pozitív egészre. Számítsuk ki \(\displaystyle f_{2022}(2022)\) értékét.

(Kanadai feladat)

(5 pont)

megoldás, statisztika

B-jelű feladatok A beküldési határidő 2022. december 12-én LEJÁRT.

---

B. 5270. \(\displaystyle n^2\) darab egységnyi oldalú szabályos háromszögből egy \(\displaystyle n\) egység oldalú háromszöget állítottunk össze, és a kis háromszögeket felváltva sötétre és világosra színeztük. A háromszögekbe beírtuk sorban az \(\displaystyle 1, 2, 3,\dots, n^2\) számokat az ábra szerint. Mennyi a sötét háromszögekbe írt számok összege?

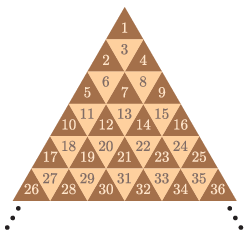
Javasolta: Németh László (Fonyód)

(3 pont)

megoldás, statisztika

---

B. 5271. Legyen \(\displaystyle ABC\) olyan egyenlő szárú derékszögű háromszög, amelyben a \(\displaystyle C\) csúcsnál van a derékszög. Jelöljük ki az \(\displaystyle AB\) oldal belsejében az \(\displaystyle A'\), a \(\displaystyle BC\) oldal belsejében a \(\displaystyle B'\) és a \(\displaystyle CA\) oldal belsejében a \(\displaystyle C'\) pontokat úgy, hogy az \(\displaystyle A'B'C'\) háromszög hasonló legyen az \(\displaystyle ABC\) háromszöghöz.

Mutassuk meg, hogy az \(\displaystyle AB\) oldal felezőpontja, az \(\displaystyle A'B'\) szakasz felezőpontja és a \(\displaystyle C\) pont egy egyenesre esik.

Javasolta: Hajdu Endre (Sopron) és Hujter Mihály (Budapest)

(3 pont)

megoldás, statisztika

---

B. 5272. Egy bolha a koordinátarendszer \(\displaystyle (a,b)\) pontjából indul, ahol \(\displaystyle a\), \(\displaystyle b\) pozitív egészek. Egy-egy ugrással balra vagy lefele mozog egységnyit. Addig ugrál, amíg el nem éri az \(\displaystyle x\) vagy az \(\displaystyle y\) tengelyt. A lehetséges ugrássorozatok hányadrésze végződik az \(\displaystyle x\) tengelyen?

Melján Dávid (Kecskemét) ötletéből

(4 pont)

megoldás, statisztika

---

B. 5273. Kijelöljük az \(\displaystyle ABC\) egyenlő oldalú háromszög \(\displaystyle AB\) oldalán a \(\displaystyle D\), a \(\displaystyle BC\) oldalán pedig az \(\displaystyle E\) pontot úgy, hogy \(\displaystyle BCD\sphericalangle=45^\circ\) és \(\displaystyle CDE\sphericalangle=30^\circ\). Mutassuk meg, hogy \(\displaystyle BE=2AD\).

Javasolta: Róka Sándor (Nyíregyháza)

(4 pont)

megoldás, statisztika

---

B. 5274. Az \(\displaystyle a<b\) pozitív egészek szorzata négyzetszám. Mutassuk meg, hogy van olyan \(\displaystyle x\) pozitív egész, amelyre \(\displaystyle a\le x^2\le b\).

Javasolta: Róka Sándor (Nyíregyháza)

(5 pont)

megoldás, statisztika

---

B. 5275. Van-e olyan irracionális \(\displaystyle a\) szám, amelyre \(\displaystyle a^{\sqrt{3}}\) racionális?

Javasolta: Hujter Bálint (Budapest)

(5 pont)

megoldás, statisztika

---

B. 5276. Bizonyítsuk be, hogy végtelen sok olyan pozitív egész \(\displaystyle k\) szám létezik, amelyre \(\displaystyle 2^k\) számjegyeinek összege

\(\displaystyle a)\) kisebb;

\(\displaystyle b)\) nagyobb,
mint \(\displaystyle 2^{k+1}\) számjegyeinek összege.

Javasolta: Sándor Csaba (Budapest)

(6 pont)

megoldás, statisztika

---

B. 5277. Az \(\displaystyle ABC\) háromszögbe írt kör középpontja \(\displaystyle I\). A \(\displaystyle BCA\) körív felezőpontja \(\displaystyle F\), az \(\displaystyle FI\) egyenes a körülírt kört másodszor az \(\displaystyle M\) pontban metszi. Mutassuk meg, hogy a \(\displaystyle CM\) egyenes átmegy a beírt és a körülírt kör külső hasonlósági pontján.

Javasolta: Kós Géza (Budapest)

(6 pont)

megoldás, statisztika

A-jelű feladatok A beküldési határidő 2022. december 12-én LEJÁRT.

---

A. 836. Minden \(\displaystyle i \in \mathbb{N}\) esetén legyen \(\displaystyle A_i\), \(\displaystyle B_i\) és \(\displaystyle C_i\) három véges és páronként diszjunkt részhalmaza \(\displaystyle \mathbb{N}\)-nek. Tegyük fel, hogy \(\displaystyle \mathbb{N}\) minden, \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) halmazokból álló partíciójához létezik \(\displaystyle i \in \mathbb{N}\) úgy, hogy \(\displaystyle A_i \subset A\), \(\displaystyle B_i \subset B\) és \(\displaystyle C_i \subset C\). Bizonyítsuk be, hogy ekkor létezik véges \(\displaystyle S \subset \mathbb{N}\) is, melyre \(\displaystyle \mathbb{N}\) minden \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) halmazokból álló partíciójához létezik \(\displaystyle i \in S\) úgy, hogy \(\displaystyle A_i \subset A\), \(\displaystyle B_i \subset B\) és \(\displaystyle C_i \subset C\).

Javasolta: Imolay András (Budapest)

(7 pont)

megoldás, statisztika

---

A. 837. Az \(\displaystyle A_1A_2A_3A_4\) tetraéder minden éle érint egy \(\displaystyle G\) gömböt; az \(\displaystyle A_i\) csúcsból a \(\displaystyle G\)-hez húzott érintőszakasz hossza legyen \(\displaystyle a_i\). Mutassuk meg, hogy

\(\displaystyle \bigg(\sum_{i=1}^4 \frac 1{a_i}\bigg)^{\!\!2}> 2\bigg(\sum_{i=1}^4 \frac1{a_i^2}\bigg). \)

Javasolta: Vígh Viktor (Szeged)

(7 pont)

megoldás, statisztika

---

A. 838. Az \(\displaystyle X\subset \mathbb{Z}^{+}\) és \(\displaystyle Y\subset \mathbb{Z}^{+}\) halmazokat bajtársiasnak nevezzük, ha minden pozitív egész \(\displaystyle n\) előáll \(\displaystyle n=xy\) alakban, ahol \(\displaystyle x\in X\) és \(\displaystyle y\in Y\). Jelöljük \(\displaystyle X(n)\)-nel és \(\displaystyle Y(n)\)-nel azt, hogy az \(\displaystyle X\) és \(\displaystyle Y\) halmazoknak hány eleme van az első \(\displaystyle n\) pozitív egész között.

Legyen \(\displaystyle f\colon \mathbb{Z}^{+}\to \mathbb{R}^{+}\) egy tetszőleges végtelenbe tartó függvény. Bizonyítsuk be, hogy léteznek olyan \(\displaystyle X\) és \(\displaystyle Y\) bajtársias halmazok, hogy \(\displaystyle \frac{X(n)}{n}\) és \(\displaystyle \frac{Y(n)}{n}\) is a \(\displaystyle 0\)-hoz tartanak, és tetszőleges \(\displaystyle \varepsilon>0\)-ra létezik olyan \(\displaystyle n \in \mathbb{Z}^+\), hogy

\(\displaystyle \frac{\min\big\{X(n), Y(n)\big\}}{f(n)}<\varepsilon. \)

(7 pont)

megoldás, statisztika