A KöMaL 2008. áprilisi matematika feladatai

Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.

Feladat típusok elrejtése/megmutatása:

C-jelű feladatok

A beküldési határidő 2008. május 15-én LEJÁRT.

C. 940. Bizonyítsuk be, hogy minden pozitív egész n esetén 2⁴ⁿ-1 és 2⁴ⁿ+1 közül valamelyik osztható 17-tel.

(5 pont)

C. 941. Egy 10 m hosszú, téglalap alakú tanterem mennyezetén két olyan lámpát helyeztünk el, amelyek kúp alakú, 90^o-os nyílásszögű fénynyalábot bocsátanak ki. Az egyik lámpa a mennyezet közepén található, és a padlón egy 6 m átmérőjű kört világít meg. A másik lámpa búráját elfordították úgy, hogy az általa megvilágított részen a terem hosszanti irányában elfér egy 10 m-es szakasz, de a két szemközti falra már nem esik fény. Milyen messze van a két lámpa egymástól?

(5 pont)

megoldás, statisztika

C. 942. Egy d differenciájú számtani sorozatban a₁=1 és a_n=81. Egy q hányadosú mértani sorozatban b₁=1 és b_n=81. Tudjuk még, hogy $\frac qd=0{,}15$ . Adjuk meg az összes ilyen sorozatot.

(5 pont)

megoldás, statisztika

C. 943. Egy körcikk területe 100. Mekkora a sugara, ha minimális a kerülete?

(5 pont)

megoldás, statisztika

C. 944. Ricsi, Dénes és Attila gyakran szoktak pingpongozni egymással úgy, hogy az egyik oldalon ketten állnak. Dénes és Attila háromszor olyan gyakran nyer Ricsi ellen, mint ahányszor veszít; Dénes ugyanolyan gyakran nyer Ricsi és Attila ellen, mint ahányszor veszít; végül Attila kétszer olyan gyakran nyer Ricsi és Dénes ellen, mint ahányszor veszít. Legutóbb egy egész délutánt játékkal töltöttek, melynek során hat meccset játszottak, minden felállásban kettőt. Mekkora annak a valószínűsége, hogy Ricsi legalább egyszer győzött, akár egyedül, akár párban?

(5 pont)

megoldás, statisztika

B-jelű feladatok

A beküldési határidő 2008. május 15-én LEJÁRT.

B. 4082. Az ábrán egy olyan síkidom látható, amellyel nem lehet egy egységsugarú félkört lefedni, de két egybevágó példányával már lefedhető egy egységsugarú kör. Létezik-e konvex síkidom is ugyanezzel a tulajdonsággal?

Kvant nyomán

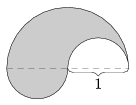
(4 pont)

megoldás, statisztika

B. 4083. Egy 10×10-es táblázat minden egyes mezőjébe egy-egy számjegyet írunk úgy, hogy minden egyes számjegy pontosan 10 mezőben szerepel. Meg tudjuk-e ezt úgy tenni, hogy minden sorban és oszlopban legfeljebb 4 különböző szám fordul elő?

Kvant

(4 pont)

megoldás, statisztika

B. 4084. Melyek azok a pozitív egész számokból álló (a_n) sorozatok, amelyekre minden i $\ne$ j esetén (a_i,a_j)=(i,j) teljesül?

(3 pont)

megoldás, statisztika

B. 4085. Igazoljuk, hogy ha egy szimmetrikus trapéz érintőnégyszög, akkor a magassága mértani közepe az alapoknak.

(3 pont)

megoldás, statisztika

B. 4086. A gömbfelületen egymástól függetlenül véletlenszerűen kiválasztunk négy pontot. Mi annak a valószínűsége, hogy az általuk meghatározott tetraéder tartalmazza a gömb középpontját?

(5 pont)

megoldás, statisztika

B. 4087. Mutassuk meg, hogy ha egy háromszög oldalainak hossza 2, 3 és 4, akkor van olyan $\alpha$ és $\beta$ szöge, amelyekre

2 $\alpha$ +3 $\beta$ =180^o.

Javasolta: Varga Zoltán (Siófok)

(3 pont)

megoldás, statisztika

B. 4088. Az AB₁B₂ hegyesszögű háromszög B₁B₂ oldalának belső pontja P. Jelöljük Q-val a P pontnak az A-ra vonatkozó tükörképét. Jelölje D_i a P pontnak az AB_i szakaszra eső merőleges vetületét, a D_iB_i szakasz felezőpontja F_i. Bizonyítsuk be, hogy ha QD₁ merőleges PF₁-re, akkor QD₂ merőleges PF₂-re.

Javasolta: Bodnár János (Budapest)

(5 pont)

megoldás, statisztika

B. 4089. Oldjuk meg az

x⁴-7x³+13x²-7x+1=0

egyenletet.

(4 pont)

megoldás, statisztika

B. 4090. Az ABC hegyesszögű háromszög A-ból induló f szögfelezője a BC oldalt D-ben, a köré írható kört E-ben metszi. A C-ből induló magasságvonal f-et M-ben, a köré írható kört Q-ban, a B-ből induló magasságvonal f-et N-ben, a köré írható kört P-ben metszi. Igazoljuk, hogy ekkor

$\frac{BD}{DC} = \frac{PE \cdot AN \cdot ME}{QE \cdot CM \cdot NP}.$

(4 pont)

megoldás, statisztika

B. 4091. Igazoljuk, hogy tetszőleges m, t pozitív egész számok esetén teljesül a következő azonosság:

$\sum_{k=0}^m \binom mk \binom{t+k}{m}=\sum_{k=0}^m\binom mk\binom tk\cdot2^k.$

(5 pont)

megoldás, statisztika

A-jelű feladatok

A beküldési határidő 2008. május 15-én LEJÁRT.

A. 452. Egy 2n csúcsú egyszerű gráfnak n²+1 éle van. Igazoljuk, hogy az élek legalább n háromszöget határoznak meg.

(5 pont)

statisztika

A. 453. A gömbfelületen egymástól függetlenül véletlenszerűen kiválasztunk n pontot. Mi annak a valószínűsége, hogy a kiválasztott pontok konvex burka tartalmazza a gömb középpontját?

(5 pont)

statisztika

A. 454. Létezik-e olyan konstanstól különböző valós együtthatós p polinom, amelyre minden x valós szám esetén p²(x)-1=p(x²+1) teljesül?

(5 pont)

statisztika

A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:

megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.

(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

Már regisztráltál?
Új vendég vagy?