KöMaL Problems in Mathematics, September 2008
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on October 10, 2008. |
K. 169. Four boys and four girls went dancing. In the first four dances, each boy danced exactly once with each girl. (They remained with the same partner during each dance, and only switched between the dances.) Charles danced the Viennese waltz with Fanny and Bernard danced it with Helen. Albert danced tango with Gaby and David with Fanny. Gaby danced mambo with Charles and Emily with David. Who were the partners dancing the first dance, the English waltz together?
(6 pont)
solution (in Hungarian), statistics
K. 170. The pattern shown in the Figure is printed on a long strip of paper. It is a polygon closing up on itself. (The Figure only shows the beginning and the end of the strip.) The length of each segment of the polygon is 1 cm. a) Is it possible that the length of the part of the strip covered by the pattern is exactly 100 cm? b) Is it possible that the total length of the line segments constituting the pattern is 2008 cm? c) Given that the area bounded by the pattern is 65 cm2, find the length of the part of the strip covered by the pattern.
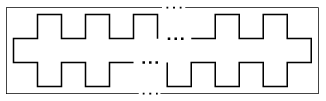
(6 pont)
solution (in Hungarian), statistics
K. 171. Four classes of 8th-grade students took part in a mathematics competition organized by a school. Each team scored a different number of points. A mathematics teacher added up the scores of two teams in every possible way and revealed that the largest sum was 128, and the smallest sum was 82. He also disclosed that the team in the second place was only 4 points ahead of the team in the third place. What was the difference between the scores of the teams in the first and four places?
(6 pont)
solution (in Hungarian), statistics
K. 172. Write the whole numbers 1 to 19 in the fields of the ``Latin hexagon'' shown in the Figure so that the sum of the numbers is the same in each column and along each diagonal row of adjacent small hexagons touching each other along a common side (whether it contains three or four of them). Find all possible solutions.
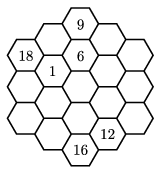
(6 pont)
solution (in Hungarian), statistics
K. 173. A knight is to be transferred from C5 to H2 on the chessboard with the smallest possible number of moves. How many steps does this way consist of? Find 12 several minimal ways. (A move means two squares in one direction and then one square at an angle of 90o.)
(6 pont)
solution (in Hungarian), statistics
K. 174. a) Is it possible for the sum of four consecutive odd numbers to be a four-digit number with all digits identical? b) Is it possible for the sum of five consecutive odd numbers to be a five-digit number with all digits identical? c) Is it possible for the sum of eight consecutive even numbers to be an eight-digit number with all digits identical?
(6 pont)
 |
Problems with sign 'C'Deadline expired on October 15, 2008. |
C. 950. In what base of notation is the multiplication 166.56=8590 correct?
(5 pont)
solution (in Hungarian), statistics
C. 951. Buildings on one side of a street are numbered with consecutive even numbers. The sum of the numbers in a block is 78. Given that there are at least 5 buildings in the block, what may be the number of the fourth building?
(5 pont)
solution (in Hungarian), statistics
C. 952. The radius of a given circle k is 5 units. P is a given point outside the circle. Construct a chord that is 8 units long and subtends a right angle at point P.
(5 pont)
solution (in Hungarian), statistics
C. 953. Given that a right-angled trapezium has an inscribed circle, show that the length of the right-angled leg is the harmonic mean of the lengths of the bases.
(5 pont)
solution (in Hungarian), statistics
C. 954. Peter's favourite CD has eleven songs on it. He likes the eighth one best. When he inserts the CD in the player, he presses a button to start the first song and then he needs to press another button seven times to reach the favourite song. If he sets the player to ``random'', the player shuffles the 11 songs and plays them in that random order. What is the probability that it takes fewer presses of buttons to reach the favourite song in this way?
Suggested by Á. Számadó
(5 pont)
 |
Problems with sign 'B'Deadline expired on October 15, 2008. |
B. 4102. Let a and b be positive integers. Is it possible that a2+4b and b2+4a are both perfect squares?
(4 pont)
solution (in Hungarian), statistics
B. 4103. On sides BC and CD of a given rectangle ABCD, construct the points P and Q, such that ABPQ forms a kite that is symmetrical to the diagonal AP.
(3 pont)
solution (in Hungarian), statistics
B. 4104. Find possible numbers a, b, c, such that (n+3)2=a.(n+2)2+b.(n+1)2+c.n2 for every positive integer n.
(3 pont)
solution (in Hungarian), statistics
B. 4105. Point A moves along one arm of an angle of vertex C and point B moves along the other arm so that CA+CB=1 remains valid. Prove that there exists a point that lies on the perpendicular bisectors of AB in all positions.
(4 pont)
solution (in Hungarian), statistics
B. 4106. Determine those quadrilaterals ABCD, such that PA2+PC2=PB2+PD2 for all points P of the plane.
(4 pont)
solution (in Hungarian), statistics
B. 4107. Solve the following simultaneous equations on the set of positive numbers:
x4+y4-x2y2=13,
x2-y2+2xy=1.
(4 pont)
solution (in Hungarian), statistics
B. 4108. The angle bisectors of a triangle intersect the circumscribed circle at the points P, Q, R. Given the points P, Q, R, construct the triangle.
(4 pont)
solution (in Hungarian), statistics
B. 4109. Prove that is an irrational number.
(5 pont)
solution (in Hungarian), statistics
B. 4110. The hexagon ABCDEF and the triangle PQR lie in the same plane. The quadrilaterals ABRQ, CDPR, EFQP are all rectangles.
a) Prove that the perpendicular bisectors of the sides BC, DE, FA are concurrent.
b) Show that there exists a triangle P'Q'R', too, for which the quadrilaterals BCR'Q', DEP'R', FAQ'P' are rectangles.
(5 pont)
solution (in Hungarian), statistics
B. 4111. Let n be a positive integer, and let a1,a2,...,an be pairwise different integers. Prove that the polynomial cannot be expressed as a product of two polynomials of integer coefficients whose degrees are at least one.
(5 pont)
 |
Problems with sign 'A'Deadline expired on November 17, 2008. |
A. 458. In space, n+1 points P1,P2,...,Pn and Q are given, n 4, no four of which are in the same plane. It is known that for each triple of distinct points Pi, Pj and Pk one can find a point Pl such that Q is interior to the tetrahedron PiPjPkPl. Show that n must be even.
4, no four of which are in the same plane. It is known that for each triple of distinct points Pi, Pj and Pk one can find a point Pl such that Q is interior to the tetrahedron PiPjPkPl. Show that n must be even.
Bulgarian competition problem
(5 pont)
A. 459. Denote by Fn the nth Fibonacci number (F0=0, F1=1, Fk+1=Fk+Fk-1). Show that one can find a positive integer n, having at least 1000 distinct prime divisors, such that n divides Fn.
Proposed by: Péter Csikvári, Budapest
(5 pont)
A. 460. If p(x) is a polynomial with degree less than 2n, show that
(5 pont)
Upload your solutions above.
