A C. 869. feladat

Rendelje meg a KöMaL-t!

ELTE

VersenyVizsga portál

Kísérletek.hu

Matematika oktatási portál

C. 869. Egy R sugarú gömbbe írt henger magassága $\frac{4}{3}R$ . Hányadrésze a henger térfogata a gömb térfogatának?

(5 pont)

A beküldési határidő LEJÁRT.

Megoldás. Jelöljük R-rel a gömb, r-rel a henger sugarát, és m-mel a henger magasságát.

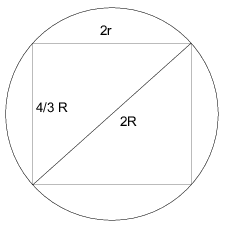
Ekkor az ábra alapján a Pitagorasz-tételt felírva:

$(2R)^2 = (2r)^2 + (\frac43R)^2,$

ahonnan

$r^2 = \frac59R^2.$

A térfogatok aránya innen

$\frac{V_{\rm{henger}}}{V_{\rm{g\"omb}}} = \frac{r^2 \pi m}{\frac{4R^3 \pi}3} = \frac{\frac{5R^2 \pi}9 \cdot \frac43R}{\frac{4R^3 \pi}3} = \frac59.$

Tehát a henger a gömb térfogatának $\frac59$ -része.

A C. 869. feladat statisztikája

570 dolgozat érkezett.

5 pontot kapott: 451 versenyző.

4 pontot kapott: 53 versenyző.

3 pontot kapott: 18 versenyző.

2 pontot kapott: 23 versenyző.

1 pontot kapott: 6 versenyző.

0 pontot kapott: 11 versenyző.

Nem versenyszerű: 8 dolgozat.

A KöMaL 2006. októberi matematika feladatai

Támogatóink:

ELTE