A KöMaL 2005. áprilisi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
C-jelű feladatokA beküldési határidő 2005. május 17-én LEJÁRT. |
C. 805. Adjuk meg azokat az egész számokból álló számhármasokat, amelyek szorzata négyszer akkora, mint az összegük, és egyikük kétszer akkora, mint a másik kettő összege.
Javasolta: Koncz Levente, Budapest
(5 pont)
C. 806. Adjuk meg az összes olyan 7-tel osztható pozitív egész számot, amelynek tízes számrendszerbeli alakja 5-re végződik és a többi jegye pedig 1.
Javasolta: Kiss Géza, Budapest
(5 pont)
C. 807. Egy négyszög két szomszédos oldalának hossza 2, illetve 1 egység, közrezárt szögük 60o. A négyszög húr- és érintőnégyszög is egyben. Mekkora a négyszög másik két oldala?
(5 pont)
C. 808. Oldjuk meg a {3x}2+{x}2=1 egyenletet.
(5 pont)
C. 809. Az egységnyi élű ABCDEFGH kocka AE élének felezőpontja P, a BCGF lap középpontja R.
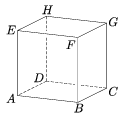
a) Mekkora területű síkidomban metszi a kockát a P, B, R pontokon átmenő sík?
b) A fenti sík két testre vágja a kockát. Mennyi a részek térfogatának az aránya?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2005. május 17-én LEJÁRT. |
B. 3812. Adjuk meg az összes olyan pozitív egész n számot, amelyre
a) 7399|n!, de 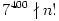 , illetve
, illetve
b) 7400|n!, de 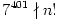 .
.
(4 pont)
B. 3813. Bizonyítsuk be, hogy tetszőleges ABC háromszög belsejében pontosan egy olyan M pont van, amelyre
MA+BC=MB+AC=MC+AB.
(4 pont)
B. 3814. Az n és k pozitív egészek, amelyekre teljesül, hogy 2kn|k2+n2-k. Bizonyítsuk be, hogy k négyzetszám.
(4 pont)
B. 3815. Egy sík metszi a térbeli, zárt P1P2...PnP1 töröttvonal mindegyik szakaszát, a PiPi+1 szakaszt annak belső Qi pontjában. Igazoljuk, hogy
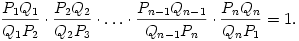
(3 pont)
B. 3816. Az ABC háromszög beírt körének középpontja O. Az AO, BO, CO szakaszok O-n túli meghosszabbításai a körülírt kört rendre az A1, B1, C1 pontokban metszik. Mutassuk meg, hogy az A1B1C1 háromszög területe
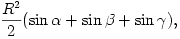
ahol R a körülírt kör sugara,  ,
,  ,
,  pedig az eredeti ABC háromszög szögei.
pedig az eredeti ABC háromszög szögei.
(4 pont)
B. 3817. Az an sorozatot a következőképpen értelmezzük:
a1 2,
2, 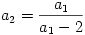 ,
, 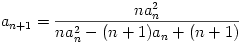 , ha n
, ha n 2.
2.
Bizonyítsuk be, hogy minden n-re teljesül az
a1+2a2+3a3+...+ nan=a1.a2.a3.....an
egyenlőség.
Javasolta: Kovács Béla, Szatmárnémeti
(5 pont)
B. 3818. Egy tetraédernek van egy olyan csúcsa, amelyből kiinduló három él mindegyike egység hosszúságú, és közülük bármely kettő 45 fokos szöget zár be egymással. Számítsuk ki a tetraéder térfogatát.
Cserti József (Budapest) javaslata alapján
(4 pont)
B. 3819. Mutassuk meg, hogy ha A1B1, A2B2 és A3B3 egy kör három párhuzamos húrja, akkor az A1, A2, illetve A3 pontból rendre a B2B3, B3B1 és B1B2 egyenesre állított merőlegesek egy ponton mennek át.
(5 pont)
B. 3820. Oldjuk meg a következő egyenletet:
(5x-2x-2)2+ 2lg (5x+2x-2)=x.
(4 pont)
B. 3821. Az a, b, c pozitív számokra a2+b2+c2=1. Határozzuk meg az
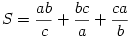
összeg legkisebb lehetséges értékét.
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2005. május 17-én LEJÁRT. |
A. 371. Az a,b,c  0 számokra teljesül, hogy a+b
0 számokra teljesül, hogy a+b c+1, b+c
c+1, b+c  a+1, c+a
a+1, c+a b+1. Mutassuk meg, hogy a2+b2+c2
b+1. Mutassuk meg, hogy a2+b2+c2 2abc+1.
2abc+1.
(5 pont)
A. 372. Az n oldalú szabályos háromszöget felosztjuk egység oldalú szabályos háromszögekre a szokásos módon. Legfeljebb hány bástyát lehet letenni az így kapott rács rácspontjaiba úgy, hogy semelyik kettő ne támadja egymást? A bástyák a tábla mezőin az oldalakkal párhuzamosan összesen hat irányban mozoghatnak.
Javasolta: Egri Attila (Hajdúszoboszló)
(5 pont)
A. 373. Az A1A2A3A4 négyszög belsejében adott egy P pont úgy, hogy nincs rajta egyik átlón sem. Legyen Bi (i=1,2,3,4) az AiP szakasz egy belső pontja. Jelölje Cij az AiBj és AjBi egyenesek metszéspontját (1 i<j
i<j  4). Bizonyítsuk be, hogy a C12C34, C13C24, C14C23 szakaszok egy ponton mennek át.
4). Bizonyítsuk be, hogy a C12C34, C13C24, C14C23 szakaszok egy ponton mennek át.
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

