A KöMaL 2007. márciusi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2007. április 10-én LEJÁRT. |
K. 121. Egy téglalap minden oldalán kijelölünk egy tetszőleges pontot. Mi a feltétele annak, hogy a pontok által meghatározott négyszög területe éppen a téglalap területének felével legyen egyenlő?
Javasolta: Szalkai Balázs (Veszprém)
(6 pont)
K. 122. Vegyünk fel egy AB szakaszt a síkon, és vizsgáljuk, hogy a sík egyes egyenesein hány olyan pont van, amivel az AB szakasz egyenlőszárú háromszöget alkot. Nevezzük ezt az egyenes ,,egyenszár'' számának. Adjuk meg az összes lehetséges ,,egyenszár'' számot.
(6 pont)
K. 123. Három nyuszi ül a fűben, mindegyikük előtt egy kupac répa, összesen 36. Ha egyazon pillanatban az első nyuszi átadná a másodiknak répái harmadát, a második a harmadiknak répái negyedét és a harmadik az elsőnek a répái ötödét, mindenkinek ugyanannyi répája lenne, mint kezdetben volt. Melyik nyuszinak hány répája van?
(6 pont)
K. 124. Pisti a reggelinél, miután egy nyolcdarabos macisajtból kettőt megevett, a megmaradt darabokat az ábrán látható elrendezésben visszatette a dobozba. Anyukája ennek nem örült, mert szerinte ,,összenyomorgatta'' a sajtokat. Pisti szerint semmi ilyesmi nem történt, a sajtok éppen visszafértek a dobozba. Melyiküknek lehet igaza?
Javasolta: Kós Géza (Budapest)
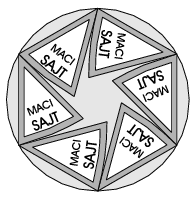
(6 pont)
K. 125. Sebi és Vince fa építőelemekből tornyokat készítettek. Mindketten egyforma négyzet alapú hasábokból építkeztek, Sebi az építőelemeket a kisebb felületű lapjaik mentén rakta egymásra, míg Vince a nagyobb felületű oldalakat illesztette egymáshoz. Sebi négy elemből álló tornya pont ugyanolyan magasra sikerült, mint Vince hat elemű építménye. Milyen magasak a tornyok, ha az alapterületük összege 160 cm2?
(6 pont)
K. 126. Az unatkozó szultán palotájában ezer szoba van. Mindegyik szobában van egy villanykapcsoló, mellyel az abban a szobában levő összes lámpát egyszerre lehet le- vagy felkapcsolni. Egyik reggel, amikor minden szobában égtek a lámpák, az unatkozó szultán elindult egy kis sétaútra. Az 1000 szobát végigjárta egyesével, majd újra és újra megtette ezt, mindig az első szobától kezdve a sétát. A kirándulás során először minden szobában kapcsolt egyet a villanykapcsolón (tehát ha fel volt kapcsolva, akkor lekapcsolta, ha le volt kapcsolva, akkor felkapcsolta), majd a sétát újrakezdve minden második szobában kapcsolt a kapcsolón, aztán ismét újrakezdve a sétát minden harmadik szobában, és így tovább. Az 500. kör után azonban elunta ezt a játékot, és elment aludni. Olyan szobát akart kiválasztani, melyben nem égnek a lámpák. Mely szobák közül választhatott?
Javasolta: Bohner Géza (Budapest)
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2007. április 16-án LEJÁRT. |
C. 890. Melyek azok a természetes számpárok, amelyek szorzata egyenlő a különbségük ötszörösével?
(5 pont)
C. 891. Legfeljebb hány oldalú lehet az a konvex sokszög, amelynek belső szögei d=1o differenciájú számtani sorozatot alkotnak?
(5 pont)
C. 892. Bizonyítsuk be, hogy ha x, y, z pozitív valós számok és xyz=1, akkor nem lehet az
kifejezések mindegyike nagyobb -nál.
(5 pont)
C. 893. Tizenhat húsvéti tojás közül három piros. Tíz tojást egy nagyobb, hatot egy kisebb dobozba helyeztünk véletlenszerűen. Mekkora annak a valószínűsége, hogy mindkét dobozban van piros tojás?
(5 pont)
C. 894. Egy félgömb alakú levesestál térfogata 8 liter. Mennyi leves tölti meg a tálat fele magasságáig?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2007. április 16-án LEJÁRT. |
B. 3982. 100 friss diplomás matematikus állást keres, ezért két fejvadász céget is felkeresnek. Mindkét cég kínálatában ugyanaz a 100 állás szerepel. Mindkét cég javaslatot tesz mindegyik jelentkezőnek, mindegyiknek különbözőt. Mindegyik jelentkező a két javaslat közül választ. Szerencsére így minden állás gazdára talál.
Három hónap próbaidő után után azonban mindenkiben felmerül a változtatás gondolata, és inkább a másik cég által ajánlott munkahelyet választja (ha ez megegyezett az éppen aktuális állással, akkor marad). Mutassuk meg, hogy ekkor ismét minden állás gazdára talál.
Javasolta: Csajbók Bence (Budapest)
(3 pont)
B. 3983. Néhányan paintball-ütközetet vívnak egymással. Egy adott helyzetben a játékosok egymástól való távolsága mind különböző. Ekkor mindenki rálő a hozzá legközelebb álló emberre. Keresztezhetik-e egymást a golyók pályái?
(3 pont)
B. 3984. Ha egy négyzetet hegyesszögű háromszögekre darabolunk, legalább hány rész keletkezik?
(5 pont)
B. 3985. Kertünkben a gyep n fűszálból áll. Úgy szeretnénk lenyírni a füvet, hogy minden fűszál egyenlő hosszú legyen, de a fűszálak összhossza ne változzék. Összesen a fűszálakon n-1 vágást végezhetünk, és a levágott darabokat egymáshoz, illetve a megmaradt részekhez ragaszthatjuk. Megoldható-e mindig a kívánalmaknak megfelelően a fűnyírás?
(4 pont)
B. 3986. Tetszőleges pozitív egész m-re jelölje s(m) az m számjegyeinek az összegét. Határozzuk meg az összes olyan n pozitív egészt, amelynek egyetlen számjegye sem nulla, és teljesíti az
s(n2)=2s(n)
összefüggést.
Javasolta: Dobribán Edgár (Kolozsvár, Báthory I. Líceum, 11. évf.)
(4 pont)
B. 3987. Legyen n 4 egész szám,
4 egész szám, pedig jelöljön nemnegatív valós számokat. Bizonyítsuk be, hogy
Vizsgáljuk meg azt is, hogy mely esetekben áll fenn egyenlőség.
(5 pont)
B. 3988. Egy konvex ötszög oldalainak felezőpontjai F1, F2, F3, F4, F5, ebben a sorrendben (az F5 és az F1 felezőpontokat tartalmazó oldalak közös csúcsa A). Legyen P az a pont a síkban, amelyre a PF2F3F4 négyszög paralelogramma. Bizonyítsuk be, hogy ekkor a PF5AF1 négyszög is paralelogramma.
(3 pont)
B. 3989. A pozitív a, b, c számokra teljesül, hogy
a2+b2+c2+abc=4.
Bizonyítsuk be, hogy a+b+c 3.
3.
(5 pont)
B. 3990. Bizonyítsuk be, hogy egy derékszögű háromszögben a hegyesszögek szögfelezőinek és a körülírt körnek a metszéspontjai, valamint a befogók és a beírt kör érintési pontjai egy egyenesen vannak.
(4 pont)
B. 3991. Az ABC egyenlőszárú háromszögben C-nél derékszög van. Legyen P a BC oldal egy tetszőleges pontja, és jelölje G a C pont AP-re való merőleges vetületét. Legyen H az AP szakasz azon pontja, amelyre AH=CG. Milyen szög alatt látszik AB felezőpontjából a GH szakasz?
(3 pont)
 |
A-jelű feladatokA beküldési határidő 2007. április 16-án LEJÁRT. |
A. 422. Legyenek pozitív valós számok, amikre
. Bizonyítsuk be, hogy
Román versenyfeladat
(5 pont)
A. 423. Határozzuk meg mindazokat az n pozitív egészeket, amikre az számok kiszínezhetők n színnel úgy, hogy mindegyik szín pontosan kétszer fordul elő, és az
számok mindegyike pontosan egyféleképpen áll elő két azonos színű szám különbségeként.
Német versenyfeladat
(5 pont)
A. 424. Adott az ABCD konvex négyszög és a belsejében a P pont úgy, hogy AP=CP, és
. Mutassuk meg, hogy
DA.AB.BP=BC.CD.DP.
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

