A KöMaL 2017. szeptemberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2017. október 10-én LEJÁRT. |
K. 547. Péter gondolt egy pozitív egész számot, és hozzáadta a fordítottját. Így olyan háromjegyű számot kapott, amiben csak 6-os és/vagy 9-es számjegy szerepel. Melyik számra gondolhatott Péter? (Például 26 fordítottja 62, 530 fordítottja 35.)
(6 pont)
K. 548. Van négy, 1-től 4-ig sorszámozott dobozunk, és négy cédulánk, melyeken sorban az 1, 2, 3, 4 számok láthatók. A négy doboz mindegyikébe egy-egy cédulát helyezünk a következő szabálynak megfelelően: minden cédula azt mutatja meg, hogy az őt tartalmazó doboz sorszámának megfelelő cédula melyik dobozban található. Hányféleképpen helyezhetjük el a dobozokban a cédulákat ennek a feltételnek megfelelően?
(6 pont)
K. 549. Egy úton három autó halad azonos irányban, mindegyik más-más sebességgel, de egyenletes tempóval. Az autók az úton egymás mögött hatféle sorrendben helyezkedhetnek el (elvileg). Létrejöhet-e útjuk során mind a hat lehetséges sorrend?
Javasolta: Loránt László (Budapest)
(6 pont)
K. 550. Egy különleges távírdában az elküldendő szavakért fizetendő összeget a benne foglalt betűk értéke határozza meg. A mássalhangzók ingyenesek, a magánhangzóknak azonban meghatározott értékük van. Ezeket az értékeket mi nem ismerjük, viszont tudjuk a következő néhány, korábban elküldött szó árát: TÉGLALAP, PARALELOGRAMMA, NÉGYZET, HÁROMSZÖG, NÉGYSZÖG, ROMBUSZ, TRAPÉZ, DELTOID. Mutassunk egy lehetséges módszert, amivel a fenti szavakért fizetendő összegek segítségével meghatározhatjuk a GEOMETRIA szóért fizetendő összeget.
(6 pont)
K. 551. Adjunk meg olyan \(\displaystyle x > y > z\) pozitív egész számokat, hogy
\(\displaystyle \frac{1}{x^{2}} + \frac{1}{y^{2}} = \frac{1}{z^{2}} \)
teljesüljön.
(6 pont)
K. 552. Melyik az a legnagyobb osztója 9900-nak, ami 22-vel, 33-mal és 55-tel osztható, azonban 44-gyel, 50-nel és 99-cel nem osztható?
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2017. október 10-én LEJÁRT. |
C. 1427. Osszunk fel egy négyzetet tíz darab egyenlő szárú, hegyesszögű háromszögre.
(Elemente der Mathematik)
(5 pont)
C. 1428. Ha négy egymás után következő páratlan szám szorzata 9-re végződik, akkor mi lehet a 9 előtt álló számjegy?
Matlap (Kolozsvár)
(5 pont)
C. 1429. Egy \(\displaystyle 5\mathrm{~cm}\times8\mathrm{~cm}\) méretű téglalapban elhelyeztünk tíz pontot. Bizonyítsuk be, hogy van két olyan pont, amelyek távolsága nem nagyobb \(\displaystyle \sqrt{10}\) cm-nél.
(5 pont)
C. 1430. Határozzuk meg azokat az \(\displaystyle x\), \(\displaystyle y\) természetes számokat, amelyekre \(\displaystyle \frac{20}{x}+\frac{17}{y}=1\) és \(\displaystyle xy\) négyzetszám.
Javasolta: Kovács Béla (Szatmárnémeti)
(5 pont)
C. 1431. Egy trapéz rövidebb alapjának, egyik, majd másik szárának, végül hosszabbik alapjának hossza ebben a sorrendben egy számtani sorozat egymást követő tagjai. Mekkora a sorozat differenciája, ha a legrövidebb oldal 3 cm, és a hosszabbik alapon fekvő egyik szög 60 fok?
(5 pont)
C. 1432. Mutassuk meg, hogy bármely \(\displaystyle n\) természetes szám esetén található olyan \(\displaystyle 2^n\)-nel osztható \(\displaystyle n\)-jegyű szám, amelynek számjegyei kizárólag 1-esből és 2-esből állnak.
(5 pont)
C. 1433. Egy csuklós szerkezet keresztmetszete négy darab \(\displaystyle r\) sugarú kör, és közöttük egy rombusz alakban kifeszülő négy, \(\displaystyle r\times6r\) oldalhosszúságú téglalap úgy, hogy a téglalapok \(\displaystyle r\) hosszú oldala érinti a kört. (Az érintési pont az oldal felezőpontjába esik.) A körök mozgatásával a rombusz szöge változhat, de a téglalapok nem lóghatnak egymásba. Mekkora a legkisebb és a legnagyobb lehetséges szög?
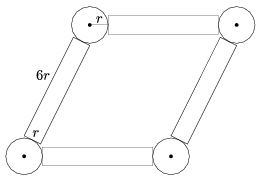
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2017. október 10-én LEJÁRT. |
B. 4885. Legyen \(\displaystyle k\) és \(\displaystyle m\) két különböző, 14-jegyű pozitív egész szám, mindkettőben 2 darab 1-es, 2-es, 3-as, 4-es, 5-ös, 6-os és 7-es számjegyet tartalmaz (mint pl. a 22133456456717). Bizonyítsuk be, hogy \(\displaystyle \frac km\) nem lehet egész.
(M&IQ)
(4 pont)
B. 4886. Hányféle konvex poliédert határoznak meg egy adott kocka csúcsai? (Két poliédert akkor tekintünk különbözőnek, ha nem egybevágók.)
(3 pont)
B. 4887. Bizonyítsuk be, hogy végtelen sok olyan \(\displaystyle (a,b)\) számpár van, amelyre \(\displaystyle a+\frac{1}{b}=b+\frac{1}{a}\), ahol \(\displaystyle a\ne b\). Adjuk meg \(\displaystyle ab\) lehetséges értékeit.
Javasolta: Szoldatics József (Budapest)
(3 pont)
B. 4888. Sebestyén a harmadiktól kezdve minden születésnapjára olyan háromszög alapú hasáb alakú tortát kap, amelynek a felső három csúcsában van egy-egy gyertya, és a tetején még annyi, hogy az életkorával megegyező számú gyertya legyen összesen a tortán úgy, hogy semelyik három nem esik egy egyenesbe. Sebestyén olyan, háromszög alakú szeletekre szeretné vágni a tortát, melyeknek a csúcsait a gyertyák helye adja (a háromszögek belseje nem tartalmazhat gyertyát). Hány szeletre oszthatja a tortát a \(\displaystyle k\)-adik születésnapján?
(4 pont)
B. 4889. Az \(\displaystyle ABCD\) érintőtrapéz beírt köre az \(\displaystyle AB\) alapot a \(\displaystyle T\), a vele párhuzamos \(\displaystyle CD\) alapot az \(\displaystyle U\) pontban érinti. Legyen \(\displaystyle M\) az \(\displaystyle AD\) és \(\displaystyle BC\) száregyenesek metszéspontja, és legyen \(\displaystyle V\) az \(\displaystyle AB\) oldal és az \(\displaystyle MU\) egyenesek metszéspontja. Mutassuk meg, hogy \(\displaystyle AT=VB\).
(4 pont)
B. 4890. Oldjuk meg a pozitív egész számok halmazán a következő egyenletet:
\(\displaystyle x-y-\frac xy-\frac{x^3}{y^3}+\frac{x^4}{y^4} = 2017. \)
Javasolta: Kovács Béla (Szatmárnémeti)
(5 pont)
B. 4891. Az \(\displaystyle S_1\), \(\displaystyle S_2\), \(\displaystyle S_3\) körök páronként kívülről érintik egymást. Legyenek \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) rendre az \(\displaystyle S_1\) és \(\displaystyle S_2\), \(\displaystyle S_1\) és \(\displaystyle S_3\), \(\displaystyle S_2\) és \(\displaystyle S_3\) körök közös pontjai. Az \(\displaystyle AB\) egyenes ismételten elmetszi az \(\displaystyle S_2\) és \(\displaystyle S_3\) köröket a \(\displaystyle D\), illetve az \(\displaystyle E\) pontokban. A \(\displaystyle DC\) egyenes újabb metszéspontja az \(\displaystyle S_3\) körrel legyen az \(\displaystyle F\) pont. Bizonyítsuk be, hogy a \(\displaystyle DEF\) háromszög derékszögű.
(Kvant)
(5 pont)
B. 4892. Kezdő és Második a következő játékot játsszák. Kezdetben 2017 kavicsot helyeznek az asztalra, először Kezdő elvesz 1 kavicsot, majd Második dönt, hogy 1 vagy 2 kavicsot vesz el. Ezután Kezdő elvesz 1, 2, 3 vagy 4 kavicsot, majd Második vesz el legalább 1, de legfeljebb 8 kavicsot. És így tovább, az \(\displaystyle i\)-edik lépésben a soron következő játékosnak legalább 1, de legfeljebb \(\displaystyle 2^{i-1}\) kavicsot kell elvennie. A játékot az nyeri, aki az utolsó kavicsot elveszi. Kinek van nyerő stratégiája?
(6 pont)
B. 4893. Az \(\displaystyle ABC\) háromszögben \(\displaystyle AB\ne BC\). A \(\displaystyle B\) pontból induló szögfelező a háromszög \(\displaystyle AC\) oldalát a \(\displaystyle D\) pontban, körülírt körét pedig (a \(\displaystyle B\) ponton kívül) az \(\displaystyle E\) pontban metszi. A \(\displaystyle DE\) szakasz, mint átmérő fölé emelt kör a körülírt kört az \(\displaystyle E\), majd másodszor az \(\displaystyle E\)-től különböző \(\displaystyle F\) pontban metszi. Bizonyítsuk be, hogy a \(\displaystyle BF\) egyenest a \(\displaystyle BD\) tengelyre tükrözve az \(\displaystyle ABC\) háromszög súlyvonalát kapjuk.
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2017. október 10-én LEJÁRT. |
A. 701. Egy légitársaság az Európai Unió bármely két tagállamának fővárosa között egy rögzített árú járatot üzemeltet (az ár oda és vissza mindig megegyezik). Tudjuk még, hogy egy városból nem indul két azonos árú járat. Anna és Bella mindegyik várost pontosan egyszer szeretné meglátogatni, nem feltétlenül ugyanabból a városból indulva. Anna úgy tervezi útját, hogy egy városból mindig abba a még nem meglátogatott városba megy tovább, amibe a lehető legolcsóbb járat vezet. Bella pedig minden városból a lehető legdrágább járaton megy tovább.
Igaz-e, hogy Bella útja biztosan legalább annyi pénzbe kerül, mint Anna útja?
(Szovjet feladat alapján)
(5 pont)
A. 702. Adott egy \(\displaystyle ABC\) háromszög. Azt mondjuk, hogy az \(\displaystyle XYZ\) háromszög esztétikus, ha \(\displaystyle X\) a \(\displaystyle BC\), \(\displaystyle Y\) a \(\displaystyle CA\), \(\displaystyle Z\) pedig az \(\displaystyle AB\) oldalszakasz pontja, valamint az \(\displaystyle XYZ\) és az \(\displaystyle ABC\) háromszög hasonló (tehát \(\displaystyle A\sphericalangle=X\sphericalangle\), \(\displaystyle B\sphericalangle=Y\sphericalangle\), \(\displaystyle C\sphericalangle=Z\sphericalangle\)). Melyik esztétikus háromszög kerülete a lehető legkisebb?
(5 pont)
A. 703. Adott egy \(\displaystyle n\ge 2\) egész szám. Egy egész számokból álló rendezett szám-\(\displaystyle n\)-est primitívnek nevezünk, hogyha a benne szereplő számok legnagyobb közös osztója \(\displaystyle 1\). Bizonyítsuk be, hogy minden primitív szám-\(\displaystyle n\)-esekből álló véges \(\displaystyle H\) halmazhoz létezik olyan nem konstans homogén egész együtthatós \(\displaystyle f(x_1,x_2,\dots,x_n)\) polinom, amelynek értéke minden \(\displaystyle H\)-beli szám-\(\displaystyle n\)-esben \(\displaystyle 1\).
Az 58. Nemzetközi Matematika Diákolimpia 6. feladata nyomán
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

