 |
Az A. 844. feladat (2023. január) |
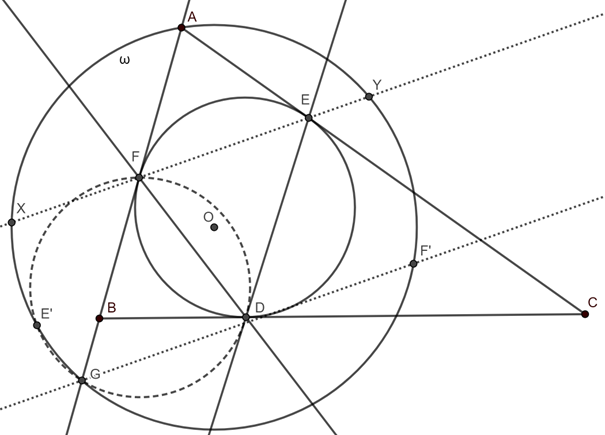
A. 844. Az \(\displaystyle ABC\) háromszög beírt köre a \(\displaystyle BC\), \(\displaystyle AC\) és \(\displaystyle AB\) oldalakat rendre a \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle F\) pontban érinti. Legyen \(\displaystyle E'\) az \(\displaystyle E\) tükörképe a \(\displaystyle DF\) egyenesre, \(\displaystyle F'\) pedig \(\displaystyle F\) tükörképe a \(\displaystyle DE\) egyenesre. Messe az \(\displaystyle EF\) egyenes az \(\displaystyle AE'F'\) háromszög köréírt körét \(\displaystyle X\)-ben és \(\displaystyle Y\)-ban. Bizonyítsuk be, hogy \(\displaystyle DX=DY\).
Javasolta: Lovas Márton (Budapest)
(7 pont)
A beküldési határidő 2023. február 10-én LEJÁRT.
Az általánosság elvesztése nélkül tegyük fel, hogy \(\displaystyle A B<A C\). Legyen \(\displaystyle \omega\) az \(\displaystyle A E^{\prime} F^{\prime}\) kör, és messe az \(\displaystyle A B\) egyenes \(\displaystyle \omega\)-t \(\displaystyle G\)-ben. Használjuk a bevett \(\displaystyle \alpha\), \(\displaystyle \beta\) és \(\displaystyle \gamma\) jelöléseket az \(\displaystyle ABC\) háromszög szögeire.
1.lemma: Az \(\displaystyle A E F^{\prime}\) és \(\displaystyle A F E^{\prime}\) háromszögek egybevágóak.
Bizonyítás: A tükrözések miatt \(\displaystyle E^{\prime} F=F E=E F^{\prime}\), valamint \(\displaystyle A E=A F\). Szögszámolással kapjuk, hogy
\(\displaystyle A E F^{\prime} \sphericalangle=A E F \sphericalangle+F E D \sphericalangle+D E F^{\prime} \sphericalangle=\left(90^{\circ}-\frac{\alpha}{2}\right)+\left(90^{\circ}-\frac{\beta}{2}\right)+\left(90^{\circ}-\frac{\beta}{2}\right)=270^{\circ}-\frac{\alpha}{2}-\beta,\)
valamint
\(\displaystyle A F E^{\prime} \sphericalangle=360^{\circ}-A F E \sphericalangle-E F D \sphericalangle-D F E^{\prime} \sphericalangle=360^{\circ}-\left(90^{\circ}-\frac{\alpha}{2}\right)-\left(90^{\circ}-\frac{\gamma}{2}\right)-\left(90^{\circ}-\frac{\gamma}{2}\right)=\)
\(\displaystyle =270^{\circ}+\frac{\alpha}{2}+\gamma-180^{\circ}=270^{\circ}+\frac{\alpha}{2}+\gamma-(\alpha+\beta+\gamma)=270^{\circ}-\frac{\alpha}{2}-\beta,\)
tehát a vizsgált háromszögekben két oldal és a közrezárt szög megyegyezik, ezzel a lemmát igazoltuk. Ebből az is világos, hogy az \(\displaystyle AEF\) és \(\displaystyle AF'E'\) háromszögek hasonlóak.
2.lemma: Az \(\displaystyle F E^{\prime} G D\) négyszög húrnégyszög.
Bizonyítás: Vegyük észre, hogy
\(\displaystyle F G E^{\prime} \sphericalangle=A G E^{\prime} \sphericalangle=A F^{\prime} E^{\prime} \sphericalangle=A E F \sphericalangle=90^{\circ}-\frac{\alpha}{2}=F D E \sphericalangle=F D E^{\prime},\)
amiből a lemma következik.
3.lemma: A \(\displaystyle D\) pont az \(\displaystyle F G F^{\prime}\) háromszög köréírt körének középpontja.
Bizonyítás: Figyeljük meg, hogy \(\displaystyle F G D \sphericalangle=F E^{\prime} D \sphericalangle=\) \(\displaystyle F E D \sphericalangle=90^{\circ}-\frac{\beta}{2}\), és \(\displaystyle G F D \sphericalangle=B F D \sphericalangle=90^{\circ}-\frac{\beta}{2}\), tehát az \(\displaystyle F D G\) háromszög egyenlőszárú, azaz \(\displaystyle F D=D G\). Továbbá a tükrözés miatt \(\displaystyle F D=D F^{\prime}\), ami befejezi a lemma bizonyítását.
4.lemma: A \(\displaystyle G F^{\prime}\) és \(\displaystyle E F\) egyenesek párhuzamosak.
Bizonyítás: Mivel \(\displaystyle A G F^{\prime} \sphericalangle=A E^{\prime} F^{\prime} \sphericalangle=A F E \sphericalangle\), ezért a két vizsgált egyenes ugyanakkora szöget zár be az \(\displaystyle AB\) egyenessel, amiből a lemma állítása következik.
Ezen lemmákkal felfegyverkezve rátérhetünk a feladatra. Legyen \(\displaystyle \omega\) középpontja \(\displaystyle O\). Két kör két metszéspontját összekötő egyenes merőleges a középpontjaikat összekötő egyenesre, tehát \(\displaystyle O D\) merőleges a \(\displaystyle G F^{\prime}\) egyenesre. Ekkor azonban \(\displaystyle O D\) az \(\displaystyle E F\) egyenesre is merőleges, és \(\displaystyle OX=OY\), vagyis \(\displaystyle O D\) éppen az \(\displaystyle XY\) szakasz felezőmerőlegese, ami bizonyítja a feladat állítását.
Statisztika:
17 dolgozat érkezett. 7 pontot kapott: Diaconescu Tashi, Elekes Dorottya, Foris Dávid, Lovas Márton, Molnár-Szabó Vilmos, Nádor Benedek, Németh Márton, Seres-Szabó Márton, Sida Li, Simon László Bence, Sztranyák Gabriella, Varga Boldizsár, Virág Rudolf, Wiener Anna. 4 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2023. januári matematika feladatai

