A B. 4470. feladat (2012. szeptember)

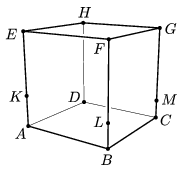
B. 4470. Az asztalon álló ABCDEFGH kocka három függőleges élét a K, L és M pontok rendre 1:2, 1:3 és 1:4 arányban osztják az ábra szerint. A KLM sík a kockát két részre vágja. Mekkora a két rész térfogatának aránya?

(5 pont)

A beküldési határidő 2012. október 10-én LEJÁRT.

Megoldás. Feltehető, hogy a kocka élei egységnyi hosszúak; ekkor AK=1/3, BL=1/4, CM=1/5. Legyen N a DH él azon pontja, amelyre DN=1/3-1/4+1/5. Ekkor $\ora{LM}=\ora{KN}$ , vagyis a K,L,M,N pontok egysíkúak, ami azt jelenti, hogy a KLM sík a DH élet N-ben metszi. Toljuk el a K és N pontokat lefelé 1/3-1/4=1/12 távolsággal. Ekkor az AK, illetve DN szakasz azon K',N' pontjaihoz jutunk, melyekre AK'=BL=1/4, DN'=CM=1/5. Mivel $\ora{LM}=\ora{KN}=\ora{K'N'}$ , a K,K',L,N,N',M pontok egy olyan háromszög alapú ferde hasáb csúcsai, melynek magassága 1, alapja pedig a KK'L háromszög, melynek területe KK'/2=1/24. Így a hasáb térfogata is 1/24.

A kocka KLMN sík alatti részéből ezt a hasábot eltávolítva a BCMLADN'K' egyenes hasábot kapjuk, melynek magassága 1, alapja pedig a BCML trapéz, melynek területe (LB+CM)/2=9/40. Így ennek a hasábnak a térfogata 9/40.

A kocka KLMN sík alatti részének térfogata tehát 1/24+9/40=32/120=4/15. A KLMN sík fölötti rész térfogata ennek megfelelően 11/15, a két rész térfogatának aránya pedig 4:11.

Statisztika:

145 dolgozat érkezett.

5 pontot kapott: 56 versenyző.

4 pontot kapott: 44 versenyző.

3 pontot kapott: 24 versenyző.

2 pontot kapott: 13 versenyző.

1 pontot kapott: 8 versenyző.

A KöMaL 2012. szeptemberi matematika feladatai

145 dolgozat érkezett.
5 pontot kapott:	56 versenyző.
4 pontot kapott:	44 versenyző.
3 pontot kapott:	24 versenyző.
2 pontot kapott:	13 versenyző.
1 pontot kapott:	8 versenyző.

Már regisztráltál?
Új vendég vagy?