 |
A B. 5146. feladat (2021. január) |
B. 5146. Adott egy egységnyi térfogatú \(\displaystyle T\) téglatest, és belsejében egy \(\displaystyle M\) pont. Tükrözzük az \(\displaystyle M\) pontot a téglatest lapsíkjaira, a kapott \(\displaystyle 6\) képpont konvex burka legyen \(\displaystyle D\). Határozzuk meg a \(\displaystyle T\cap D\) test térfogatát.
(5 pont)
A beküldési határidő 2021. február 15-én LEJÁRT.
Megoldás. Először is állapítsuk meg, hogy a tükörképek konvex burka egy \(\displaystyle D\) duplagúla, melynek kombinatorikus struktúrája az oktaéderével megegyező.
Helyezzük el a téglatestet az első térnyolcadban úgy, hogy az egyik csúcsa az \(\displaystyle O\) origó legyen, és az erre a csúcsra illeszkedő lapsíkok legyenek a koordináta-síkok. Ekkor az origóval átellenes csúcs \(\displaystyle (a,b,c)\), ahol \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle c\) a téglatest élei, \(\displaystyle abc=1\) a feltétel szerint.
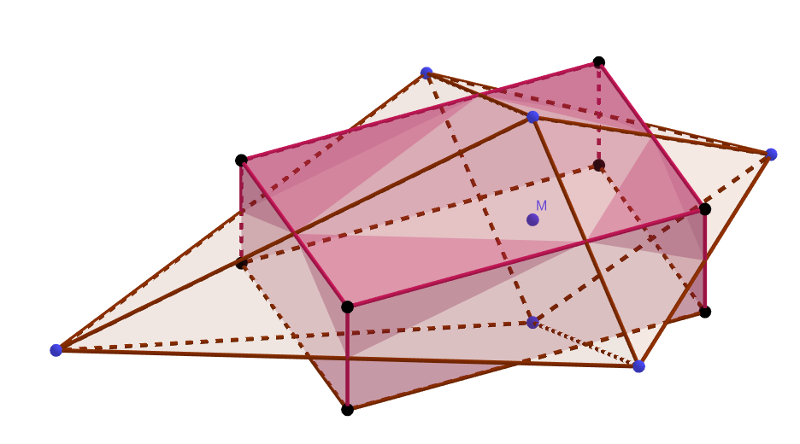
Tükrözzük az \(\displaystyle M(x_0,y_0,z_0)\) pontot a koordináta-síkokra, így értelemszerűen kapjuk az \(\displaystyle M'_{xy}(x_0,y_0,-z_0)\), \(\displaystyle M'_{xz}(x_0,-y_0,z_0)\) és \(\displaystyle M'_{yz}(-x_0,y_0,z_0)\) pontokat. Behelyettesítéssel ellenőrizhetjük, hogy ezen tükörképek mindegyike illeszkedik az
\(\displaystyle \frac x{x_0}+\frac y{y_0} + \frac z {z_0}=1\)
síkra. Ebből következik, hogy az \(\displaystyle M'_{xy}\), \(\displaystyle M'_{xz}\) és \(\displaystyle M'_{yz}\) tükörképekre illeszkedő lapsíkja \(\displaystyle D\)-nek a koordináta-tengelyeket rendre \(\displaystyle x_0\), \(\displaystyle y_0\) és \(\displaystyle z_0\) pontjaiban metszi. Ezek nyilvánvalóan épp az \(\displaystyle M\) pont vetületei a tengelyeken.
A fenti számolást mindeegyik csúcsra elvégezve következik, hogy a \(\displaystyle T\cap D\) metszet a következőképp származtatható: vetítsük le \(\displaystyle M\)-et a \(\displaystyle T\) téglatest minden élére, majd vágjuk le \(\displaystyle T\)-ből minden csúcsát a csúcsból induló élekre eső vetületek által meghatározott síkkal. Így \(\displaystyle T\)-ből összesen \(\displaystyle 8\) darab egymásba nem nyúló (esetleg csúcsokban érintkező) ``saroktetraédert'' vágunk le, ezek páronként merőleges élhármasainak hossza \(\displaystyle \{x_0,y_0,z_0\}\); \(\displaystyle \{a-x_0,y_0,z_0\}\);\(\displaystyle \{a-x_0,b-y_0, z_0\}\); stb.
Az eddigiek alapján:
$$\begin{align*} V(T\cap D)& =V(T)-V_{\text{saroktetraéderek}}=\\ & =1-\frac{x_0y_0z_0+(a-x_0)y_0z_0+x_0(b-y_0)z_0+x_0y_0(c-z_0)}{6}-\\ & -\frac{(a-x_0)(b-y_0)z_0+(a-x_0)y_0(c-z_0)+x_0(b-y_0)(c-z_0)+(a-x_0)(b-y_0)(c-z_0)}{6}=\\ & =1-\frac{abc}{6}=\frac 56. \end{align*}$$A \(\displaystyle T\cap D\) poliéder térfogata tehát \(\displaystyle 5/6\) térfogategység.
Megjegyzés. A saroktetraéderek térfogatainak összegét számolás nélkül is meghatározhatjuk, ha észrevesszük, hogy a derékszögű csúcsaiknál összeillesztve egy \(\displaystyle D\)-hez hasonló duplagúlát kapunk, amelynek testátlói éppen \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle c\), térfogata pedig \(\displaystyle abc/6=1/6\).
Statisztika:
A KöMaL 2021. januári matematika feladatai
