A B. 5173. feladat (2021. április)

B. 5173. Az \(\displaystyle ABC\) hegyesszögű háromszög magasságpontja \(\displaystyle H\), körülírt körének középpontja \(\displaystyle O\). Legyen \(\displaystyle D\) és \(\displaystyle E\) az \(\displaystyle AB\), illetve \(\displaystyle AC\) szakasz belső pontja. Az \(\displaystyle ADE\) háromszög magasságpontja és körülírt körének középpontja \(\displaystyle H'\), illetve \(\displaystyle O'\). Mutassuk meg, hogy a \(\displaystyle HH'\) és \(\displaystyle OO'\) egyenesek akkor és csak akkor párhuzamosak, ha \(\displaystyle BD = CE\).

Javasolta: Bán-Szabó Áron (Budapest)

(6 pont)

A beküldési határidő 2021. május 10-én LEJÁRT.

Megoldás. Először is vegyük észre, hogy az \(\displaystyle O\) és \(\displaystyle O'\) pontok nem eshetnek egybe, mert például \(\displaystyle D\) belső pontja az \(\displaystyle ABC\) körnek, így \(\displaystyle OD<OA\), míg \(\displaystyle O'D=O'A\). Ezért az \(\displaystyle OO'\) szakasz nem fajulhat egy ponttá. Mivel \(\displaystyle EAD\sphericalangle=CAB\sphericalangle\) hegyesszög, az \(\displaystyle ABC\) és az \(\displaystyle ADE\) háromszög magasságpontja sem lehet az \(\displaystyle A\) pont, tehát \(\displaystyle H\ne A\) és \(\displaystyle H'\ne A\).

Legyen \(\displaystyle BC\) felezőpontja \(\displaystyle F\), \(\displaystyle DE\) felezőpontja \(\displaystyle F'\), és legyen az \(\displaystyle ABC\), \(\displaystyle ADE\) körök második metszéspontja \(\displaystyle M\). Az \(\displaystyle M\) pont az \(\displaystyle AB,AC,BC,DE\) egyenesek Miquel-pontja; egyben annak a forgatva nyújtásnak a középpontja, amely a \(\displaystyle BC\) szakaszt a \(\displaystyle DE\) szakaszba viszi. Az triviális, hogy \(\displaystyle F\) képe \(\displaystyle F'\). A kerületi és középponti szögek tételéből \(\displaystyle BOC\sphericalangle = 2BAC\sphericalangle = 2DAE\sphericalangle = DO'E\sphericalangle\), a \(\displaystyle BCO\) és a \(\displaystyle DEO'\) egyenlő szárú háromszögek hasonlók és körüljárásuk is megegyezik. Emiatt a forgatva nyújtás \(\displaystyle O\)-t \(\displaystyle O'\)-be viszi.

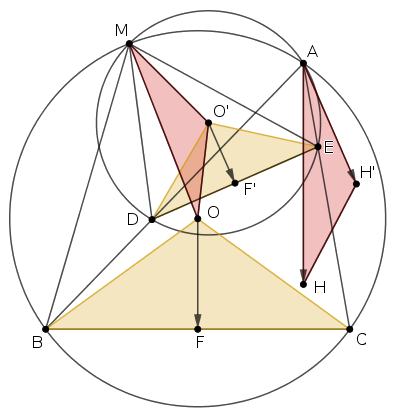
Jól ismert, hogy az \(\displaystyle ABC\) háromszögben \(\displaystyle \overrightarrow{AH}=\overrightarrow{OH}-\overrightarrow{OA}= \overrightarrow{OB}+\overrightarrow{OC}=2\overrightarrow{OF}\), és hasonlóan, az \(\displaystyle ADE\) háromszögben \(\displaystyle \overrightarrow{AH'}=2\overrightarrow{O'F'}\). Mivel az \(\displaystyle \overrightarrow{OF}\) vektor forgatva nyújtott képe az \(\displaystyle \overrightarrow{O'F'}\) vektor, ebből következik, hogy az \(\displaystyle AH\) vektor forgatva nyújtott képe az \(\displaystyle AH'\) vektor. Továbbá, az \(\displaystyle \overrightarrow{MO}\) vektor forgatva nyújtott képe az \(\displaystyle \overrightarrow{MO'}\) vektor, és ebből azt látjuk, hogy az \(\displaystyle AHH'\) (esetleg egyenes szakasszá fajuló) háromszög hasonló az \(\displaystyle MOO'\) háromszöghöz és azonos körüljárású vele. Ebből az is következik, hogy a \(\displaystyle HH'\) szakasz sem fajulhat egy ponttá.

Ezek után \(\displaystyle OO'\parallel HH'\) ekvivalens azzal, hogy \(\displaystyle MO\parallel AH\); mivel \(\displaystyle AH\perp BC\), ez akkor és csak akkor igaz, ha \(\displaystyle MO\perp BC\), vagyis ha \(\displaystyle M\) a körülírt kör valamelyik \(\displaystyle BC\) ívének felezőpontja.

Az \(\displaystyle M\) pont annak a forgatva nyújtásnak is középpontja, amely a \(\displaystyle BD\) szakaszt a \(\displaystyle CE\) szakaszba viszi, ezért \(\displaystyle MBD\triangle\sim MCE\triangle\); ezért \(\displaystyle BD=CE\) akkor és csak akkor teljesül, ha \(\displaystyle BM=CM\), ami szintén akkor igaz, ha \(\displaystyle M\) valamelyik \(\displaystyle BC\) körív felezőpontja.

Statisztika:

33 dolgozat érkezett.
6 pontot kapott:	Bán-Szabó Áron, Baski Bence, Bencsik Ádám, Bencsik Dávid, Bognár 171 András Károly, Diaconescu Tashi, Duchon Márton, Fekete Richárd, Hegedűs Dániel, Kalocsai Zoltán, Kercsó-Molnár Anita, Koleszár Domonkos, Kovács 129 Tamás, Kökényesi Márk Péter, Mohay Lili Veronika, Molnár-Szabó Vilmos, Móricz Benjámin, Nádor Benedek, Páhán Anita Dalma, Romaniuc Albert-Iulian, Seres-Szabó Márton, Simon László Bence, Somogyi Dalma, Terjék András József, Varga Boldizsár, Wiener Anna, Zömbik Barnabás.
5 pontot kapott:	Csizmadia Miklós, Lovas Márton, Virág Rudolf.
4 pontot kapott:	3 versenyző.

A KöMaL 2021. áprilisi matematika feladatai