A B. 5463. feladat (2025. május)

B. 5463. Adott a pozitív körüljárású \(\displaystyle ABCD\) négyzet. Szerkesztendő olyan, szintén pozitív körüljárású, \(\displaystyle BEF\) szabályos háromszög, amelynek \(\displaystyle F\) csúcsa a \(\displaystyle B\) kezdőpontú, \(\displaystyle C\)-t tartalmazó félegyenesre esik, és amelyre \(\displaystyle EAF\sphericalangle=45^\circ\) teljesül.

Javasolta: Vígh Viktor (Sándorfalva)

(3 pont)

A beküldési határidő 2025. június 10-én LEJÁRT.

Megoldás. Adott szabályos háromszöghöz a feladat feltételének megfelelő négyzet szerkesztése jóval kényelmesebb feladat. Először ezt végezzük el.

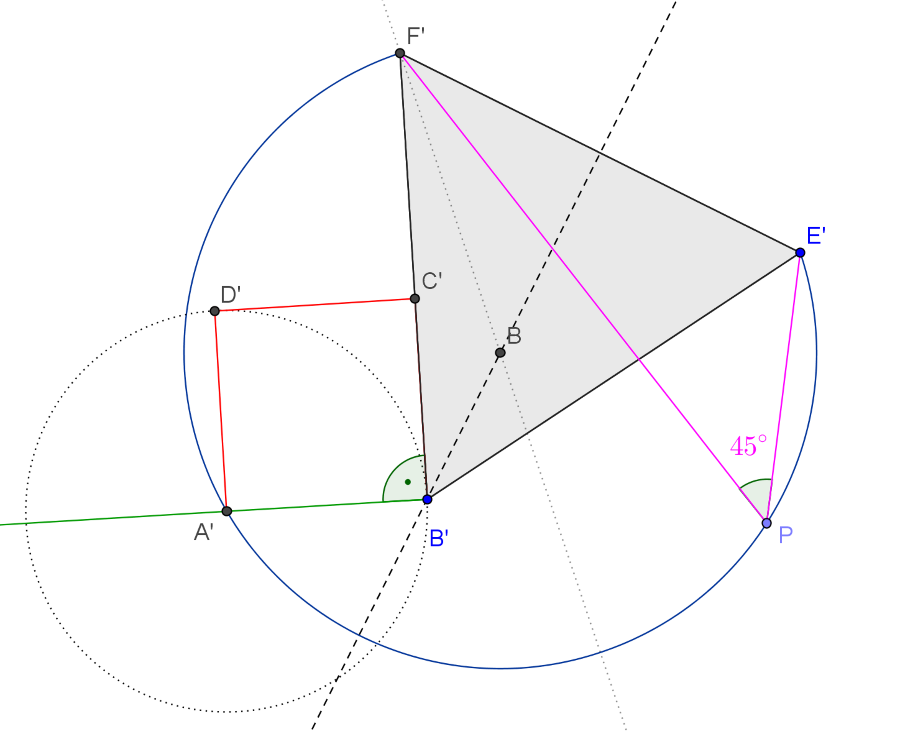
Vegyünk fel egy tetszőleges méretű, pozitív körüljárású \(\displaystyle B'E'F'\) szabályos háromszöget. Ennek \(\displaystyle E'F'\) oldala a szerkesztendő négyzet \(\displaystyle A'\) csúcsából \(\displaystyle 45^\circ\)-os szögben látszik, azaz az \(\displaystyle E'F'\) szakasz \(\displaystyle 45^\circ\)-os látókörívének pontja. A \(\displaystyle B'\) pontban a szabályos háromszög oldalára állított merőleges félegyenes kimetszi a megfelelő \(\displaystyle A'\) pontot a látókörívből. Ezután az ábrát \(\displaystyle \frac{AB}{A'B'}\) arányban nagyítva (vagy kicsinyítve) azonnal megkapjuk a megfelelő szabályos háromszög oldalának hosszúságát, és azt az előírt módon felmérhetjük a megadott négyzet \(\displaystyle BC\) oldalára, majd megszerkeszthetjük a keresett szabályos háromszöget. Világos, hogy pontosan egy megoldás van.

Statisztika:

33 dolgozat érkezett.
3 pontot kapott:	Balla Ignác , Baran Júlia, Bencze Mátyás, Bogdán Balázs Ákos, Bolla Donát Andor, Bui Thuy-Trang Nikolett, Csató Hanna Zita , Gyenes Károly, Hicsó Máté Kristóf, Hideg János, Hodossy Réka, Horák Zsófia, Kerekes András, Li Mingdao, Maróti Bálint, Molnár Lili, Nagypál Katóca, Pázmándi József Áron, Péter Hanna, Rajtik Sándor Barnabás, Sajter Klaus, Sánta Gergely Péter, Sütő Áron, Szabó 721 Sámuel, Szaszkó Benedek, Várhegyi Hanna, Wágner Márton, Zhai Yu Fan.
2 pontot kapott:	Bodor Ádám, Sárdinecz Dóra.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2025. májusi matematika feladatai