A C. 1180. feladat (2013. szeptember)

C. 1180. Vizsgáljuk meg, hogy egy hegyesszögű háromszögbe írható négyzetek közül melyiknek az oldala a legnagyobb.

Javasolta: Gyimesi Róbert

(5 pont)

A beküldési határidő 2013. október 10-én LEJÁRT.

Megoldás. Először határozzuk meg a háromszög \(\displaystyle a\) oldalára illesztett négyzet oldalának hosszát. Az \(\displaystyle AKI\) és az \(\displaystyle ABC\) háromszögek szögei egyenlők, ezért hasonlóak, és így \(\displaystyle \frac xa=\frac{m_a-x}{m_a}\), amiből \(\displaystyle x=\frac{am_a}{a+m_a}\).

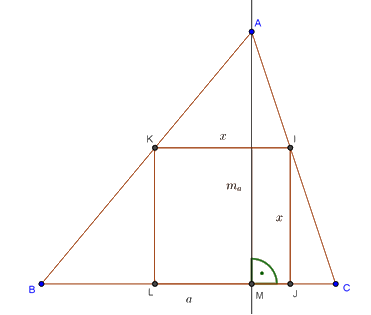
Tekintsük például az \(\displaystyle a<b\) esetet. Azt kell eldöntenünk, hogy az \(\displaystyle \frac{am_a}{a+m_a}\) és a \(\displaystyle \frac{bm_b}{b+m_b}\) hosszúságú szakaszok melyike a nagyobb. Mivel \(\displaystyle am_a=2t=bm_b\), ahol \(\displaystyle t\) az \(\displaystyle ABC\) háromszög területét jelöli, ezért elegendő a törtek nevezőjét összehasonlítanunk. Ennek érdekében tekintsük a két nevező eltérését:

\(\displaystyle a+m_a-(b+m_b)=a-b+\frac{2t}{a}-\frac{2t}{b}=(a-b)\left(1-\frac{2t}{ab}\right)\leq0,\)

hiszen a szorzat első tényezője negatív, a második pedig nem negatív (\(\displaystyle m_a\leq b\) miatt ugyanis \(\displaystyle 2t=am_a\leq ab\)). (Egyenlőség csak \(\displaystyle a\perp b\) esetén teljesülhet.)

Arra jutottunk tehát, hogy \(\displaystyle a<b\) esetén az \(\displaystyle a+m_a\) összeg nem lehet nagyobb a \(\displaystyle b+m_b\) összegnél, ebből kifolyólag az \(\displaystyle a\) oldalon "nyugvó" négyzet oldala legalább akkora, mint a \(\displaystyle b\) oldalra "támaszkodóé".

Statisztika:

47 dolgozat érkezett.
5 pontot kapott:	Bereczki Zoltán, Farkas Dóra, Hegel Patrik, Horváth Bendegúz, Kovács 972 Márton, Orbán Szandra, Sziegl Benedek, Tóth Zsófia.
4 pontot kapott:	Barna Kinga, Meleg András, Németh Klára Anna, Pammer Tamás, Temesvári Fanni, Tomai Fanni.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	17 versenyző.

A KöMaL 2013. szeptemberi matematika feladatai