Problem C. 1819. (September 2024)

C. 1819. Let \(\displaystyle ABCD\) be a unit square, and let \(\displaystyle k\) be the circle with center \(\displaystyle A\) and radius \(\displaystyle AC\). Let \(\displaystyle E\) and \(\displaystyle F\) be the points of intersection of circle \(\displaystyle k\) and rays \(\displaystyle AB\) and \(\displaystyle AD\), respectively. Let line \(\displaystyle EF\) intersect \(\displaystyle BC\) at point \(\displaystyle G\), and let \(\displaystyle H\) be the reflection of point \(\displaystyle B\) across line \(\displaystyle AG\). Find the length of line segment \(\displaystyle HE\) in the given unit.

Proposed by Dániel Hegedűs, Gyöngyös

(5 pont)

Deadline expired on October 10, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Tekintsük a következő ábrát:

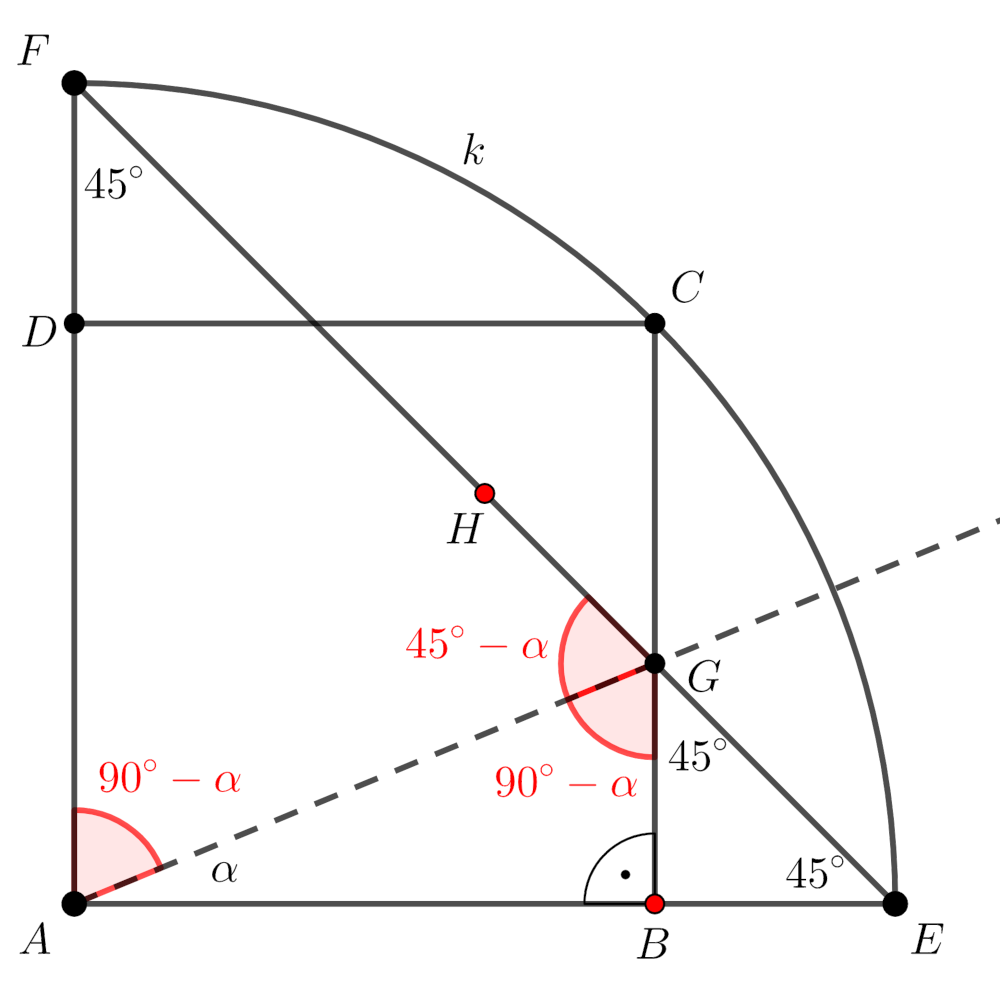
Tudjuk, hogy \(\displaystyle ABCD\) egységnyi oldalú négyzet, ezért \(\displaystyle AB=BC=CD=DA=1\), tehát \(\displaystyle AC=\sqrt{2}\). Az \(\displaystyle AEF\) háromszög egyenlő szárú és derékszögű, így \(\displaystyle AEF\sphericalangle=AFE\sphericalangle=45^{\circ}\), ezért a \(\displaystyle BEG\) derékszögű háromszög egyik hegyesszöge \(\displaystyle 45^{\circ}\), ami azt jelenti, hogy a \(\displaystyle BEG\) is egyenlő szárú derékszögű háromszög. Az előzőek alapján felírható, hogy

\(\displaystyle AF=AC=AE=r = \sqrt{2},\)

\(\displaystyle EF= \sqrt{2}AE=2,\)

\(\displaystyle BE=BG = \sqrt{2}-1,\)

\(\displaystyle EG = \sqrt{2}BG=2-\sqrt{2}.\)

Azt már láttuk (1) alapján, hogy az \(\displaystyle FAG\) háromszög \(\displaystyle AF\) oldala \(\displaystyle \sqrt{2}\), ugyanakkor az \(\displaystyle FG\) oldalát felírva a (2) és a (4) segítségével azt kapjuk, hogy \(\displaystyle \displaystyle{FG=EF-EG=2-(2-\sqrt{2})=\sqrt{2}}\). Ez azt jelenti, hogy az \(\displaystyle FAG\) háromszög egyenlő szárú, tehát

\(\displaystyle FAG\sphericalangle=AGF\sphericalangle,\)

amiből az következik, hogy

\(\displaystyle AGF\sphericalangle=AGB\sphericalangle.\)

Vagyis a \(\displaystyle B\) pont \(\displaystyle AG\) egyenesre vonatkozó tükörképe éppen az \(\displaystyle FE\) egyenesre esik, vagyis \(\displaystyle H\in FE\).
Így tehát

\(\displaystyle HE=HG+GE=BG+GE=\sqrt{2}-1+2-\sqrt{2}=1.\)

Statistics:

206 students sent a solution.
5 points:	Abonyi Donát Tibor, Balogh Péter, Bencze Mátyás, Benedek Kinyó, Bense Tamás, Budai Máté, Csáki Anikó, Csiszár András, Danka Emma, Elekes Panni, Farkas András, Gaál Gergely, Gál András, Göőz Lilla, Gyöngyösi Dorottya, Halmosi Dávid, Hetyei Dániel, Hicsó Máté Kristóf, Hollósi Dominik, Iván Máté Domonkos, Kókai Ákos, Kudomrák Lili Anna , Li Mingdao, Lovas Márk, Magura Anna Luca, Major Csilla, Maróti Olga, Masa Barnabás, Mateas Isabelle, Mezei Marcell, Miszori Márton, Molnár Lili, Nagypál Katóca, Nelissen Sámuel Zalán, Oláh András, Ördög Dávid, Palásthy Bánk, Pánovics Máté, Papp Emese Petra, Pázmándi Renáta , Pink István, Radošická Emma, Rózsa Zsombor, Szabó Máté, Szalóki Árpád, Tóth Luca, Török Eszter Júlia, Viczián Adél, Wodala Gréta Klára.
4 points:	19 students.
3 points:	19 students.
2 points:	25 students.
1 point:	30 students.
0 point:	37 students.
Not shown because of missing birth date or parental permission:	15 solutions.

Problems in Mathematics of KöMaL, September 2024