 |
A G. 884. feladat (2025. március) |
G. 884. Egy \(\displaystyle r\) sugarú, \(\displaystyle 1{,}5\) törésmutatójú üvegből készült félgömbre az ábra szerinti \(\displaystyle A\) pontban fénysugarat ejtünk. A megtört fénysugár a félgömb síklapját a középponttól \(\displaystyle y\) távolságban éri el.
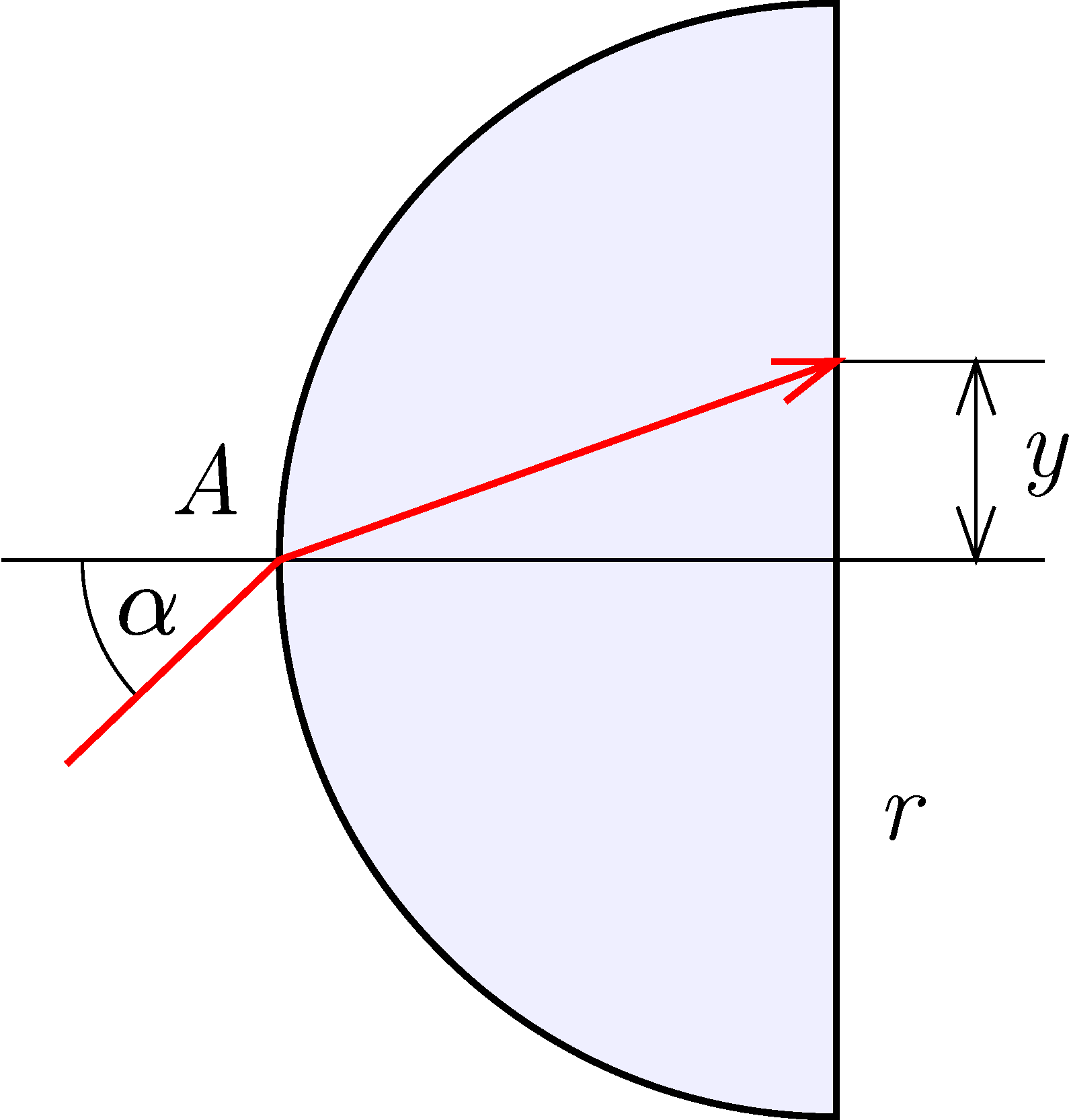
a) Mekkora beesési szög esetén lesz \(\displaystyle y\) a sugár felével egyenlő?
b) Milyen színű a fénysugár, ha a fény hullámhossza az üvegben \(\displaystyle 400\,\mathrm{nm}\)?
(3 pont)
A beküldési határidő 2025. április 15-én LEJÁRT.
Megoldás. a) Ha \(\displaystyle y\) a sugár fele, akkor a törési szög tangense 1/2. Ennek megfelelően a törési szög: \(\displaystyle \beta=26{,}6^\circ\). Írjuk fel a Snellius–Descartes-törvényt:
\(\displaystyle \frac{\sin{\alpha}}{\sin{\beta}}=n\qquad\Rightarrow\qquad\alpha=42{,}1^\circ.\)
Tehát a beesési szög \(\displaystyle 42{,}1^\circ\).
Megjegyzés. A beeső fénysugár és a félgömb \(\displaystyle A\) ponton átmenő sugara meghatároz egy síkot. Ebben a síkban halad az üvegben az \(\displaystyle A\) ponton átmenő megtört fénysugár.
b) Mivel a törésmutató \(\displaystyle n=1{,}5\), így a fény hullámhossza levegőben \(\displaystyle n\cdot 400\,\mathrm{nm}=600\,\mathrm{nm}\). A fény frekvenciája üvegben és levegőben megegyezik, értéke \(\displaystyle 5\cdot 10^{14}\,\mathrm{Hz}\). Ennek megfelelően a fény színe narancssárga.
Statisztika:
29 dolgozat érkezett. 3 pontot kapott: Békési Máté, Blaskovics Bálint, Csáki Anikó, Hegedüs Márk, Hollósi Dominik, Horváth Zsombor, Kiss Lukács Dániel, Kovács Tamás , Lakatos Levente, Majer Veronika, Molnár Sámuel , Németh Ábel, Patócs 420 Péter, Rácz Koppány Bendeguz, Sándor Ákos, Szabó Milos Farkas, Szighardt Anna, Szilaj Petra, Szűcs Kitti, Tóth Domonkos, Vízhányó Janka. 2 pontot kapott: József Áron, Kossár Benedek Balázs, Kovács Artúr-Lehel, Medgyesi András, Sógor-Jász Soma. 1 pontot kapott: 1 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2025. márciusi fizika feladatai

