A K. 881. feladat (2025. december)

K. 881. Andris, Bori, Csaba, Dóri, Egon, Fanni és Gábor egy táborban találkoztak. Andris Fanni kivételével mindenkit ismert közülük, Borinak három ismerőse volt, Csabának egy, Dórinak pedig feleannyi, mint Egonnak. Fanninak eggyel kevesebb ismerőse volt, mint Gábornak. (Az ismeretségek kölcsönösek.) Kit ismerhetett közülük Fanni a tábor kezdetén?

(5 pont)

A beküldési határidő 2026. január 12-én LEJÁRT.

Megoldás. Fanni nem ismerhette Andrist, mert a feladat szerint Andris nem ismerte őt, és az ismeretségek kölcsönösek. Nem ismerhette Csabát sem, mivel Csabának csak egy ismerőse volt, és az Andris. Bárki mást viszont ismerhetett. Ha a személyeket pöttyökkel és a kezdőbetűikkel jelöljük és az egymást ismerőket összekötjük egy-egy szakasszal, akkor az alábbi két ábra mindegyike megfelel a feladat feltételeinek, tehát bármelyik ábrázolhatja a kezdeti ismeretségeket.

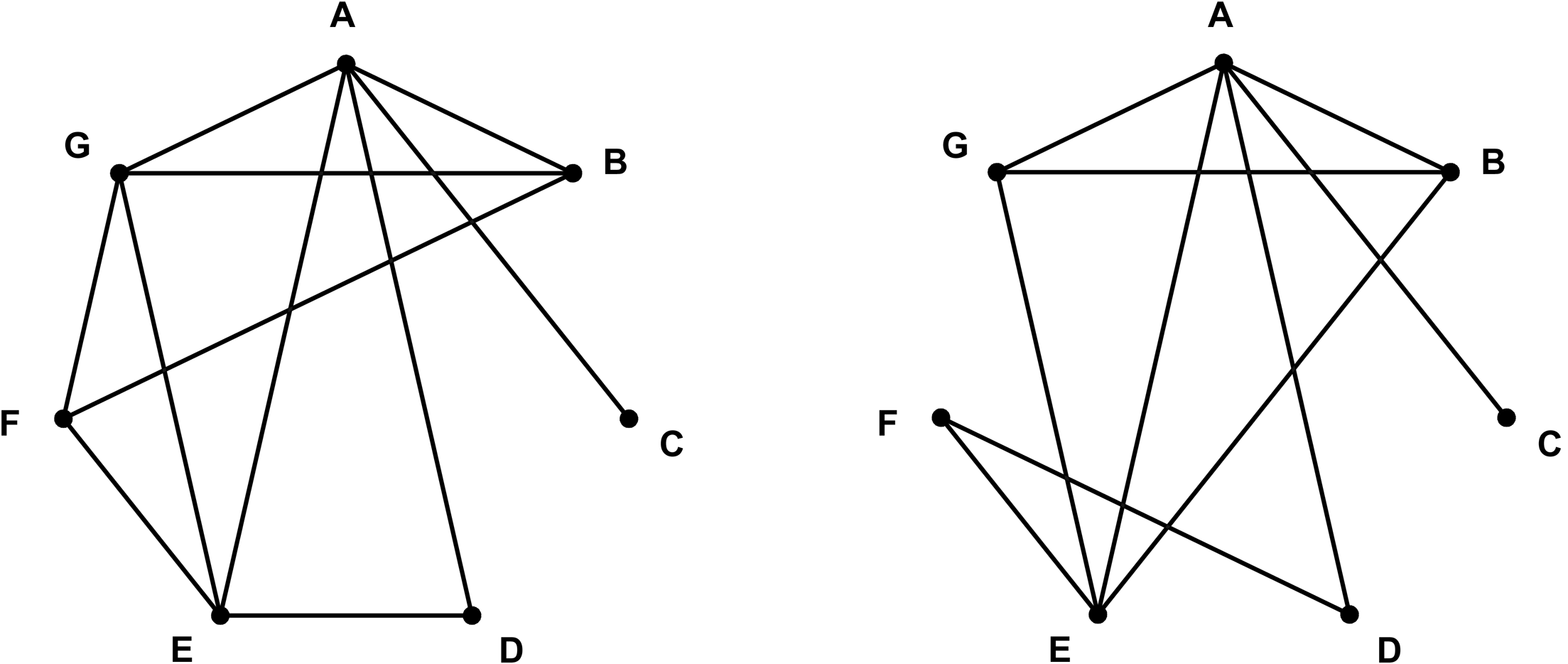
Az első ábra szerinti ismeretségek esetén Fanni Borit, Egont és Gábort ismeri, a második esetén Dórit és Egont, vagyis Andrison és Csabán kívül tényleg bárkit ismerhetett.

Megjegyzés: Összesen 12 olyan páronként különböző ismeretségi helyzet van, ami megfelel a feltételeknek. De ezek mindegyikének megtalálása – és annak bizonyítása, hogy több lehetőség nincs! – jóval nehezebb feladat, mint a kitűzött.

Statisztika:

A K. 881. feladat értékelése még nem fejeződött be.

A KöMaL 2025. decemberi matematika feladatai