 |
A P. 4677. feladat (2014. november) |
P. 4677. Az ábrán látható, könnyen gördülő kiskocsira szerelt \(\displaystyle \alpha=30^\circ\)-os lejtőhöz érintőlegesen \(\displaystyle R=20\) cm sugarú körív keresztmetszetű pálya csatlakozik. A kiskocsi és a lejtő össztömege \(\displaystyle M=0{,}5\) kg. A pálya mindenhol súrlódásmentesnek tekinthető. A \(\displaystyle 2R\) magas lejtő tetejére egy pontszerűnek tekinthető, \(\displaystyle m=0{,}3\) kg tömegű testet helyezünk, majd lökésmentesen elengedjük.
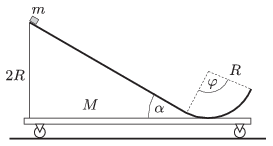
\(\displaystyle a)\) Mekkora lesz a kis test és a kiskocsi elmozdulása, sebessége és gyorsulása abban a pillanatban, amikor a kis test emelkedő mozgása során a legmagasabbra kerül, ha a körlejtő középponti szöge \(\displaystyle \varphi=120^\circ\)?
\(\displaystyle b)\) Mekkora lesz a kis test és a kiskocsi elmozdulása és sebessége abban a pillanatban, amikor a kis test éppen elhagyja a körlejtőt, ha \(\displaystyle \varphi=90^\circ\)?
Közli: Holics László, Budapest
(5 pont)
A beküldési határidő 2014. december 10-én LEJÁRT.
Megoldás: \(\displaystyle a)\) A kiskocsi balra mozdul el 36 cm-t, a kis test jobbra 59 cm-t és a kiindulási helyzetével azonos magasságba kerül. Mindkét test sebessége nulla lesz, a kiskocsi gyorsulása nulla, a kis testé pedig \(\displaystyle g\).
\(\displaystyle b)\) A kiskocsi balra mozdul el 34 cm-t, a kis test jobbra 57 cm-t, függőlegesen lefelé pedig 30 cm-rel mélyebbre kerül. A kiskocsi sebessége a kérdéses pillanatban 0,48 m/s, a kis test sebessége jobbra 0,80 m/s, függőlegesen felfelé pedig 2,2 m/s.
Statisztika:
42 dolgozat érkezett. 5 pontot kapott: Asztalos Bogdán, Balogh Menyhért, Bekes Nándor, Berta Dénes, Blum Balázs, Csathó Botond, Fehér Balázs, Forrai Botond, Fülöp Erik, Holczer András, Jakus Balázs István, Juhász 326 Dániel, Körmöczi Dávid, Nenezic Patrick Uros, Olosz Balázs, Sal Kristóf. 4 pontot kapott: Bugár 123 Dávid, Di Giovanni Márk, Iván Balázs, Lőrincz Zoltán, Marosvári Kristóf. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 10 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2014. novemberi fizika feladatai

