 |
A P. 5134. feladat (2019. május) |
P. 5134. Igen vékony, elhanyagolható tömegű, \(\displaystyle R= 0{,}64\) m hosszú rúd egyik vége vízszintes tengelyhez csatlakozik, a másik végén egy \(\displaystyle m=5\) g tömegű, \(\displaystyle Q=6\cdot10^{-7}\) C töltésű gömböcske van rögzítve. Az egész szerkezetet függőlegesen lefelé irányuló, \(\displaystyle E=2\cdot10^5\) V/m erősségű homogén elektromos térben helyezzük el. A rudat az ábra szerint vízszintes helyzetbe hozzuk.
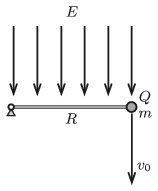
\(\displaystyle a)\) Mekkora függőlegesen lefelé mutató \(\displaystyle v_0\) sebességet kell adnunk a gömböcskének, hogy miután a rúd \(\displaystyle 3/4\) fordulatot megtéve megakad, és egyben megszűnik a gömböcske rögzítése, további mozgása során visszakerüljön a kiindulási pontjába?
\(\displaystyle b)\) Mekkora szöget zár be a vízszintessel a sebessége, amikor áthalad ezen a ponton?
\(\displaystyle c)\) Mekkora a kiindulási helyre való érkezési és indulási sebességek nagyságának aránya?
Közli: Holics László, Budapest
(5 pont)
A beküldési határidő 2019. június 11-én LEJÁRT.
Megoldás. A gömböcskére függőlegesen lefelé ható,
\(\displaystyle F=mg+QE=m\left(g+\frac{QE}{m}\right)\)
nagyságú erő hat. Ez az erő olyan, mintha csak a nehézségi erő hatna, de a gravitációs gyorsulás nem a szokásos nagyságú, hanem
\(\displaystyle g'=g+\frac{QE}{m}= \left( {9,81}+\frac{(6\cdot10^{-7})(2\cdot10^{5})}{ 5\cdot10^{-3} } \right)\frac{\rm m}{\rm s^2}=33{,}8~\frac{\rm m}{\rm s^2}\)
lenne.
\(\displaystyle a)\) Legyen a gömböcske sebessége a pályájának legmagasabb pontjánál \(\displaystyle v_1\). Ha visszajut a kiindulási helyére, a vízszintes hajítás összefüggései szerint fennáll, hogy
\(\displaystyle v_1t=R, \qquad \frac{g'}{2}t^2=R,\)
ezekből
\(\displaystyle v_1=\sqrt{\frac{g'R}{2}}\)
következik. Másrészt a munkatétel szerint
\(\displaystyle \frac{1}{2}mv_1^2-\frac{1}{2}mv_0^2=-mg'R,\)
vagyis
\(\displaystyle v_0=\sqrt{v_1^2+2g'R}=\sqrt{\frac52g'R}=7{,}36~\frac{\rm m}{\rm s}.\)
\(\displaystyle b)\) A kiindulási helyére visszaérkező test vízszintes sebessége \(\displaystyle v_1\), függőleges sebessége pedig \(\displaystyle R\) magasságból történő szabadesés sebessége, vagyis
\(\displaystyle v_2=\sqrt{2g'R}.\)
A test sebességvektora tehát
\(\displaystyle \arctg\frac{v_2}{v_1}=\arctg 2=63{,}4^\circ \)
nagyságú szöget zár be a vízszintessel.
\(\displaystyle c)\) A kiindulási helyre való visszaérkezéskor a sebesség nagysága:
\(\displaystyle v_3=\sqrt{v_1^2+v_2^2}=\sqrt{\frac52g'R}=7{,}36~\frac{\rm m}{\rm s},\)
ami éppen \(\displaystyle v_0\)-lal egyezik meg. Ez az eredmény a munkatételből közvetlenül is leolvasható. A kérdezett arány tehát 1.
Statisztika:
40 dolgozat érkezett. 5 pontot kapott: Bekes Barnabás, Békési Ábel, Bokor Endre, Bonifert Balázs, Bukor Benedek, Endrész Balázs, Fekete Levente, Fiam Regina, Fonyi Máté Sándor, Jánosik Áron, Keltai Dóra, Kertész Balázs, Ludányi Levente, Mácsai Dániel, Makovsky Mihály, Marozsák Tádé, Máth Benedek, Molnár Mátyás, Morvai Orsolya, Olosz Adél, Sal Dávid, Sümegi Géza, Tiefenbeck Flórián, Toronyi András, Varga Vázsony, Vass Bence, Vaszary Tamás, Viczián Anna, Zámbori Zalán. 4 pontot kapott: Elek Péter, Györgyfalvai Fanni, Lipták Gergő, Németh Csaba Tibor, Schneider Anna. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 2 versenyző.
A KöMaL 2019. májusi fizika feladatai
