A P. 5222. feladat (2020. április)

P. 5222. Két jó minőségű, tömör gumiból készült labdát az ábrán látható módon egymás tetejére teszünk, majd \(\displaystyle h\) magasságból elengedjük őket. A talajjal, illetve egymással történő ütközésüket közelítőleg a következő módon írhatjuk le: először az alsó, \(\displaystyle M\) tömegű labda ütközik tökéletesen rugalmasan a talajjal, majd ezt követően igen rövid idő múlva a talajról visszapattanó labda tökéletesen rugalmasan ütközik a felső, \(\displaystyle m\) tömegű labdával.

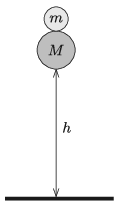
\(\displaystyle a)\) Milyen \(\displaystyle m/M\) tömegarány esetén kapja meg a felső labda a rendszer teljes kezdeti helyzeti energiáját? Milyen magasra pattan a felső labda ebben az esetben?

\(\displaystyle b)\) Milyen \(\displaystyle m/M\) tömegarány esetén pattan fel legmagasabbra a felső labda, és mekkora ez a magasság?

\(\displaystyle c)\) Milyen \(\displaystyle m/M\) tömegarány esetén alkalmazhatjuk az ütközések fenti leírását? Mi történik például a \(\displaystyle k = m/M = 3\) tömegarány esetén?

(Az ütközéseket pillanatszerűnek tekinthetjük. A labdák mérete sokkal kisebb a \(\displaystyle h\) magasságnál.)

Közli: Kis Tamás, Heves

(5 pont)

A beküldési határidő 2020. május 11-én LEJÁRT.

Megoldás. A labdák \(\displaystyle v_0=\sqrt{2gh}\) nagyságú sebességgel érik el a talajt, majd az alsó labda sebességirányt vált. Legyen a felfelé mutató irány pozitív. A két labda tökéletesen rugalmas ütközése alatt (az összenyomódási szakasz végén) a labdák elérnek egy közös \(\displaystyle c=\frac{M-m}{M+m} v_0\) sebességet, majd úgy lökődnek szét, hogy a szétlökődés során a \(\displaystyle \Delta v\) sebességváltozásuk ugyanakkora, mint az összenyomódás közben. Az alsó labda sebességváltozása \(\displaystyle \Delta v_\text{alsó}=c-v_0\), a felső labdáé \(\displaystyle \Delta v_\text{felső}=c-(-v_0 )=c+v_0.\) Az ütközés utáni sebességek tehát így adódnak:

\(\displaystyle v_\text{alsó}=c+(c-v_0 )=2c-v_0=\frac{M-3m}{M+m}\, v_0\)

és

\(\displaystyle v_\text{felső} =c+(c+v_0 )=2c+v_0=\frac{3M-m}{M+m}\, v_0 .\)

\(\displaystyle a)\) A két labda kezdeti helyzeti energiája akkor alakul át teljesen a felső labda energiájává, ha az alsó labda megáll. A fenti képletek alapján ez \(\displaystyle \frac{m}{M}= \frac{1}{3} \) tömegarány esetén valósul meg. Ezt könnyen ellenőrizhetjük, hiszen a kezdeti helyzeti energia \(\displaystyle (m+M)gh=4mgh\), míg a felső labda ütközés utáni mozgási energiája ilyen tömegarány esetén:

\(\displaystyle \frac12mv_\text{felső}^2=\frac12 m \left(\frac{3M-m} {M+m}\, v_0 \right)^2=\frac12 m\left(\frac{2m}{m}\,v_0 \right)^2=2mv_0^2=4mgh. \)

Ebben az esetben a felső labda \(\displaystyle 2v_0\) sebességgel pattan fel, és így \(\displaystyle 4h\) magasságra jut.

\(\displaystyle b)\) A felső labda ütközés utáni sebességét a \(\displaystyle k = m/M\) tömegaránnyal is kifejezhetjük:

\(\displaystyle v_\text{felső}=\frac{ 3M-m}{M+m} v_0=\frac{3-k}{1+k}\, v_0 .\)

Beláthatjuk, hogy a fenti kifejezésben lévő tört (a fizikailag reális \(\displaystyle k>0\) értékeknél) akkor maximális, ha \(\displaystyle k\approx 0\), tehát akkor repül a legmagasabbra a felső labda, ha tömege elhanyagolhatóan kicsi az alsó labda tömegéhez képest. Ebben az esetben a felső labda végsebessége \(\displaystyle 3v_0\), tehát a maximálisan elérhető magasság \(\displaystyle 9h\).

Megjegyzés. Sok sportban történik ütő-labda ütközés. Ha az ütő tömegéhez képest elhanyagolható a labda tömege, akkor az ütő sebességváltozása elhanyagolható, míg merőleges ütés esetén a labdának az ütőhöz viszonyított sebessége előjelet vált. Ha az álló labdát találja el a \(\displaystyle v\) sebességű ütő, akkor az ütőhöz képest \(\displaystyle -v\) sebességű labda sebessége vált előjelet, és a labda a talajhoz képest \(\displaystyle 2v\) sebességgel pattan el. Ha a \(\displaystyle v\) sebességű ütőhöz képest \(\displaystyle -v\) sebességgel közeledik a labda, akkor az ütőhöz képest \(\displaystyle -2v\) sebességű labda sebessége változik az ellentettjére, tehát a talajhoz képest a labda sebessége \(\displaystyle 3v\) lesz.

\(\displaystyle c)\) Szigorúan véve csak akkor alkalmazhatjuk a feladat szövegében leírt ütközési modellt, ha a két labda csak egyszer ütközik. Írjuk fel a labdák ütközés utáni sebességeit:

\(\displaystyle v_\text{alsó}= \frac{M-3m}{M+m}\, v_0= \frac{1-3k}{1+k} \, v_0,\)

\(\displaystyle v_\text{felső}= \frac{3M-m}{M+m}\, v_0=\frac{3-k}{1+k}\, v_0 .\)

Abban az esetben, ha \(\displaystyle k<\tfrac13\) , akkor az ütközés után mindkét labda felfelé repül, a felső gyorsabban, mint az alsó. Ha \(\displaystyle k=\tfrac13\), akkor (ahogy ezt már láttuk fentebb) az alsó labda megáll, a felső viszont felrepül. Ha \(\displaystyle k\) egy kissé nagyobb\(\displaystyle \tfrac13\)-nál, akkor az alsó labda visszapattan, újra ütközik a talajjal, de utána nem éri utol a felső labdát.

Akkor következik be a két labda között a második ütközés is, ha a talajról visszapattanó alsó labda utoléri a felsőt. Ennek a feltétele ez:

\(\displaystyle -\frac{1-3k}{1+k} v_0>\frac{3-k}{1+k}\,v_0,\)

amiből következik, hogy \(\displaystyle k>1\). Ha \(\displaystyle k\) éppen 1, vagyis a két labda tömege megegyezik, akkor az ütközéskor sebességet cserélnek, majd az alsó labda visszapattan a talajról, és a továbbiakban együtt szállnak a magasba, de már nem érintkeznek többet. Tehát a két labda akkor ütközik egyszer, ha \(\displaystyle k\le1\).

Tegyük fel, hogy az ütközési modell még akkor is jó, ha a labdák kétszer is ütköznek, de háromszor már nem. Ilyenkor \(\displaystyle k>1\). Nincs mit tenni, a második ütközés utáni sebességeket is ki kell számolni, mert csak így deríthetjük ki a harmadik ütközés feltételét. Hosszabb számolás után erre juthatunk:

\(\displaystyle v_\text{alsó,2}=\frac{10k-5k^2-1}{(1+k)^2}\, v_0,\)

\(\displaystyle v_\text{felső,2}=\frac{10k-k^2-5}{(1+k)^2} \, v_0 .\)

Eredményünket ellenőrizhetjük például a \(\displaystyle k = m/M = 3\) tömegarány esetében. Ilyenkor az első ütközés után a felső labda megáll, az alsó pedig \(\displaystyle 2v_0\) sebességgel pattan vissza róla, majd a talajról történő visszapattanás után az álló labdát \(\displaystyle 2v_0\) sebességgel találja el. A rugalmas ütközéskor a köztes közös sebesség \(\displaystyle v_0/2\) lesz, tehát a második ütközés után a felső labda \(\displaystyle v_0\) sebességgel indul el felfelé, míg az alsó szintén \(\displaystyle v_0\) sebességgel, de lefelé indul. Lényegében ugyanaz történik, mint a \(\displaystyle k = \tfrac13\) esetben, hiszen ilyenkor is végül a két labda azonos \(\displaystyle v_0\) sebességgel fog felfelé mozogni. Ha behelyettesítünk a fenti képletekbe, akkor megnyugtató módon ugyanezekre a számértékekre jutunk:

\(\displaystyle v_\text{alsó,2}(k=3))= \frac{10k-5k^2-1}{(1+k)^2}\, v_0=-v_0,\)

\(\displaystyle v_\text{felső,2}(k=3))= \frac{10k-k^2-5}{(1+k)^2} \, v_0=v_0.\)

Ezek szerint arra jutottunk, hogy akkor következik be a két labda között harmadik ütközés is, ha \(\displaystyle k>3.\)

Összefoglalva tehát arra jutottunk, hogy \(\displaystyle k\le 1\) esetén a két labda csak egyszer ütközik, \(\displaystyle 1<k\le3\) esetében kétszer ütköznek a labdák, míg \(\displaystyle k>3\) esetén kettőnél többször. Minél többszörös az ütközés, annál kevésbé realisztikus a feladat szövegében leírt ütközési sorozat, mert a labdák középpontjának mozgásiránya el fog térni a függőlegestől.

Statisztika:

32 dolgozat érkezett.
5 pontot kapott:	Bokor Endre, Bonifert Balázs, Fekete Levente, Kertész Balázs, Ludányi Levente, Szabados Noémi, Szabó 314 László, Tóth Ábel.
4 pontot kapott:	Békési Ábel, Fekete András Albert, Györgyfalvai Fanni, Horváth 999 Anikó, Jánosik Máté, Mócza Tamás István, Nguyễn Đức Anh Quân, Somlán Gellért, Téglás Panna, Toronyi András, Vakaris Klyvis, Vass Bence, Viczián Anna.
3 pontot kapott:	6 versenyző.
2 pontot kapott:	5 versenyző.

A KöMaL 2020. áprilisi fizika feladatai