 |
A P. 5484. feladat (2023. április) |
P. 5484. Kétatomos gázzal egy olyan körfolyamatot valósítunk meg, melynek képe a \(\displaystyle p\) – \(\displaystyle V\) síkon, a tengelyek megfelelő skálázása esetén, éppen az ábrán látható kör.
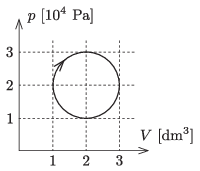
Határozzuk meg numerikus módszerekkel egy így elkészített hőerőgép hatásfokát!
Közli: Széchenyi Gábor, Budapest
(5 pont)
A beküldési határidő 2023. május 15-én LEJÁRT.
I. megoldás. Válasszuk a nyomás egységének a \(\displaystyle 10^4\) Pa értéket, a térfogategység pedig legyen a dm\(\displaystyle ^3\). Ebben az egységrendszerben a munka és a hő egysége 10 J, a kör sugara pedig éppen 1 egység lesz.
Számítógépen (pl. a Geogebra program segítségével) ábrázoljuk a
\(\displaystyle (p-2)^2+(V-2)^2=1\)
egyenletű kört, valamint a
\(\displaystyle pV^{7/5}=K=\text{állandó}\)
egyenletű adiabatikus görbéket. A \(\displaystyle K\) paraméter értékét változtatva (ezt a program ,,csúszka'' eszközével tehetjük meg) megkereshetjük azt a két adiabatát, amelyik (felülről vagy alulról) érinti a kört (lásd az 1. ábrát).
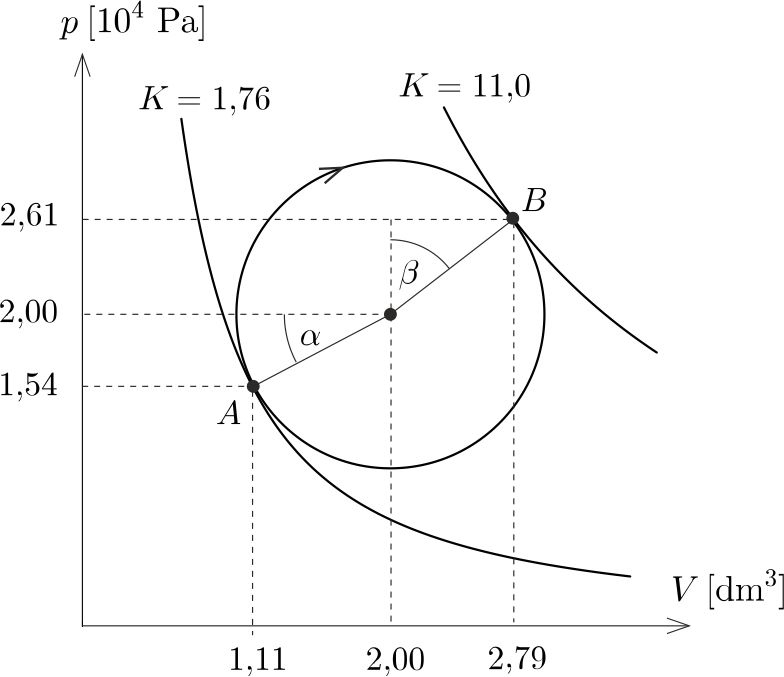
1. ábra
A körfolyamat hatásfokának kiszámításához szükségünk van a felvett hő nagyságára, valamint a gáz által egy-egy ciklusban végzett munkára. Ez utóbbi a kör területe:
\(\displaystyle W'=3{,}14.\)
Hőfelvétel az \(\displaystyle A\) és \(\displaystyle B\) állapotok között történik, ezen az íven egyre nagyobb \(\displaystyle K\) értékekhez tartozó adiabatákat metsz el a kör. Az ábráról (annak kinagyított változatáról) leolvashatjuk az \(\displaystyle A\) és \(\displaystyle B\) pont koordinátáit, és ezekből kiszámíthatjuk az ábrán jelölt szögeket:
\(\displaystyle \alpha=\arctg \frac{2{,}00-1{,}54}{2{,}00-1{,}11}=27{,}3^\circ=0{,}48\ \rm rad,\)
illetve
\(\displaystyle \beta=\arctg \frac{ 0{,}79}{ 0{,}61}=52{,}3^\circ =0{,}91\ \rm rad.\)
A folyamat során a gáz által felvett hő az I. főtétel szerint
\(\displaystyle Q_\text{fel}=W'(A\rightarrow B)+\Delta E,\)
ahol
\(\displaystyle \Delta E=E_B-E_A=\frac52\left(p_BV_B-p_AV_A\right)=18{,}2-4{,}3=13{,}9\)
a kétatomos gáz belső energiájának megváltozása (\(\displaystyle 10^4\ {\rm Pa}\cdot 1\ {\rm dm}^3=10\ \rm J\) egységekben mérve).
Hátra van még a \(\displaystyle W'(A\rightarrow B)\) munkavégzés kiszámítása. Ez a \(\displaystyle p-V\) diagramon az állapotváltozást leíró görbe (esetünkben körív) alatti, előjelesen értendő terület (növekvő térfogat esetén pozitív, csökkenőnél negatív az előjele).
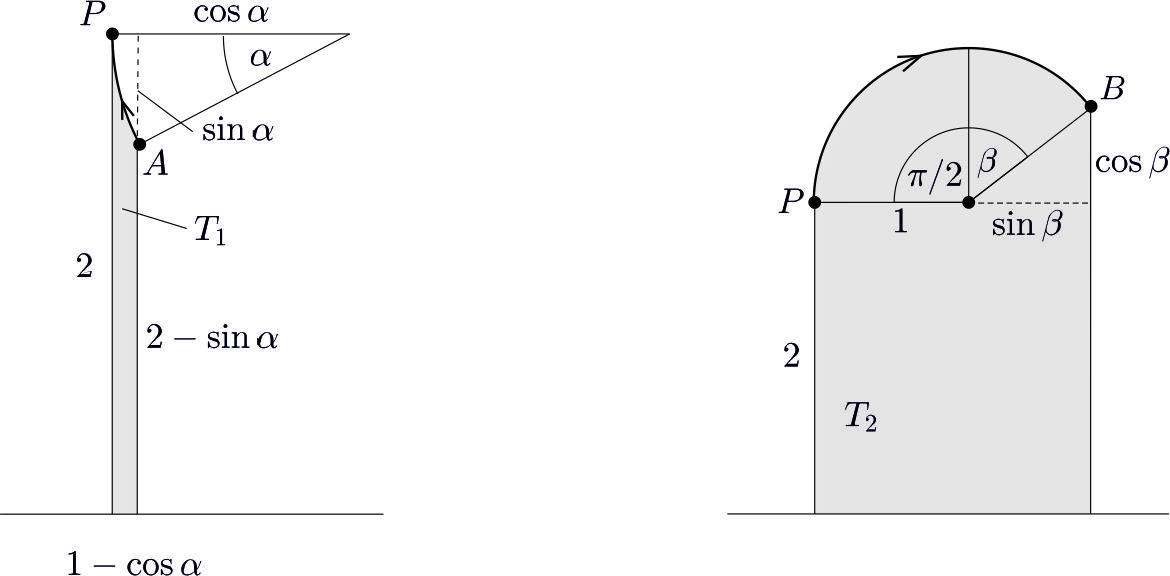
2. ábra
A 2. ábráról leolvashatjuk, hogy mindkét terület egy téglalap, egy körcikk és egy derékszögű háromszög területének összege/különbsége:
\(\displaystyle T_1=2(1-\cos\alpha)-\frac12 \alpha+\frac12\sin\alpha\,\cos\alpha=0{,}2,\)
illetve
\(\displaystyle T_2=2(1+\sin\beta)+\frac12 \left(\frac\pi2+\beta\right)+\frac12\sin\beta\,\cos\beta =5{,}1.\)
A teljes munkavégzés a hőfelvétel alatt
\(\displaystyle W'(A\rightarrow B)=T_2-T_1=4{,}9,\)
a felvett hő pedig
\(\displaystyle Q_\text{fel}=4{,}9+13{,}9=18{,}8.\)
A ,,kör alakú'' körfolyamatot végző hőerőgép termikus hatásfoka tehát
\(\displaystyle \eta=\frac{W'}{Q_\text{fel}}=\frac{3{,}14}{18{,}8}=0{,}167\approx 17\%.\)
II. megoldás. A körfolyamat mentén vegyünk fel egyenletesen \(\displaystyle N\) darab pontot. Ekkor az előző megoldásban szereplő egységeket használva az \(\displaystyle i\). ponthoz tartozó nyomás és térfogat értékek:
\(\displaystyle p_i=2-\sin{\left(2\pi\frac{i}{N}\right)},\)
\(\displaystyle V_i=2+\cos{\left(2\pi\frac{i}{N}\right)},\)
ahol \(\displaystyle i\) egész szám, mely 1-től \(\displaystyle N\)-ig vehet fel értékeket.
Tekintsük a körfolyamat egy kis körív alakú szakaszát, melyet az \(\displaystyle i+1\). és \(\displaystyle i\). pont határol. Ezen a szakaszon az energia megváltozása
\(\displaystyle \Delta E_i = \frac{5}{2}\left(p_{i+1}V_{i+1}-p_iV_i\right).\)
Amennyiben \(\displaystyle N\) kellően nagy, akkor ezen kicsiny folyamat során a gázon végzett munka jól közelíthető egy trapéz területével. Azaz az \(\displaystyle i\). és \(\displaystyle i+1\). pontot egy egyenessel kötjük össze a görbe vonal helyett:
\(\displaystyle W_i=-\frac{p_i+p_{i+1}}{2}\left(V_{i+1}-V_{i}\right).\)
A kicsiny folyamat során a rendszerrel közölt hő mennyisége az I. főtétel alapján:
\(\displaystyle Q_i=\Delta E_i + W_i.\)
Ha ez az érték pozitív, akkor hőfelvétel, ha negatív, akkor hőleadás történik.
Akár egy Excel táblázat segítségével kiszámolhatjuk az összes kicsiny folyamatra a felvett (és negatív előjellel a leadott) hőmennyiségeket, melyek közül a pozitívakat kell összegeznünk, hogy a körfolyamat egésze során felvett hőt meghatározzuk. A számolás során figyelni kell, hogy a ciklikusság miatt az \(\displaystyle (N+1)\)-edik és az első pont megegyezik. \(\displaystyle N=10\) esetében \(\displaystyle Q_\textrm{fel}=18{,}7\), növelve az \(\displaystyle N\) értékét \(\displaystyle N=50\) esetében \(\displaystyle Q_\textrm{fel}=18{,}8\), még tovább növelve \(\displaystyle N=100\) esetében (három jegy pontossággal) az eredmény ugyanannyi: \(\displaystyle Q_\textrm{fel}=18{,}8\). Látható, hogy a felbontás finomításával hamar konvergál az érték.
A felvett hő meghatározása után az előző megoldás alapján számolhatjuk a hatásfokot.
Statisztika:
15 dolgozat érkezett. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 4 versenyző.
A KöMaL 2023. áprilisi fizika feladatai

