A KöMaL 2018. novemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2018. december 10-én LEJÁRT. |
M. 381. Készítsünk A4-es írólapból (vagy annak egy részéből) ragasztással papírhengert! Gurítsuk le a hengert az asztal tetején elhelyezett, éppen az asztal széléig érő lejtőről!
Mérjük meg, milyen messzire érkezik egy csúszásmentesen legördülő papírhenger az asztal szélének függőleges vetületétől! Hogyan függ ez a távolság a papírhenger átmérőjétől? Eredményeinket hasonlítsuk össze egy forgás nélkül lecsúszó és leeső kicsiny test (például egy pénzérme) vízszintes irányú elmozdulásával!
Közli: Gnädig Péter, Vácduka
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2018. december 10-én LEJÁRT. |
G. 649. Ha a gőzfürdőben mozgunk (például karjainkkal legyezni kezdünk), akkor a 40–60 \(\displaystyle ^\circ\)C-os gőzt a szokásosnál sokkal melegebbnek, szinte égetőnek érezzük. Miért?
(3 pont)
G. 650. Áron azzal szórakozott, hogy a 30 cm hosszú, egyenes vonalzója végére tette a kicsi radírját, és az asztal szélére merőlegesen csúsztatta kifelé a vonalzót. Megmérte, hogy ha 11 cm-nél jobban kitolja, akkor a vonalzó lebillen. Mekkora a vonalzó és a radír tömegének aránya?
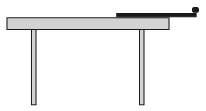
(3 pont)
G. 651. Az óceánjáró hajók oldalán látható az úgynevezett Plimsoll-jel. Ez megmutatja, hogy milyen mélyen merül be a vízbe a hajó a különböző vizekben, ha a megengedett maximális tömegű rakománnyal terhelik. (TF = Tropical Fresh Water; F = Fresh Water; T = Tropical Seawater; S = Summer Seawater; W = Winter Seawater; WNA = Winter North Atlantic.)
A legfelső, TF jelű vonal a trópusi édesvíz (sűrűsége 996 kg/m\(\displaystyle {}^3\)) esetén érvényes bemerülést jelzi, alatta a mérsékelt övi édesvíz (sűrűsége 999 kg/m\(\displaystyle {}^3\)) esetén érvényes, F jelű vonal látható. Egy bizonyos hajón a két vonal távolsága 7 cm. Mekkora a téli tengervíz sűrűsége, ha a W feliratú, a téli tengervízben érvényes vonal a legfelső vonaltól 21 cm-rel lejjebb van?
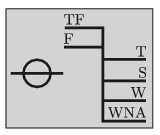
(4 pont)
G. 652. Egy test nyugalomból indulva egy egyenes mentén mozog úgy, hogy gyorsulása időben egyenletesen növekszik a kezdeti zérus értékről másodpercenként 2 m/s\(\displaystyle ^2\) értékkel. Mekkora a test sebessége az indulást követően 4 másodperc múlva?
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2018. december 10-én LEJÁRT. |
P. 5067. Egy súrlódásmentes rúdra felfűzünk két könnyű rugót, amelyek rugóállandója \(\displaystyle D_1\), illetve \(\displaystyle D_2\). A rugók egyik vége rögzített, másik végeik közötti távolság \(\displaystyle d\). A rúdra felfűzött \(\displaystyle m\) tömegű, kis méretű testtel együtt az egyik rugót \(\displaystyle x\)-szel összenyomjuk, majd a testet elengedjük.
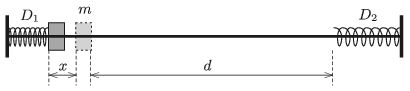
Mennyi idő múlva tér vissza elindulási helyére az \(\displaystyle m\) tömegű kis test? Függ-e ez az idő attól, hogy melyik rugóról indítjuk a testet?
Közli: Kobzos Ferenc, Dunaújváros
(4 pont)
P. 5068. Egy kicsiny, pontszerűnek tekinthető, \(\displaystyle m\) tömegű üstökös közeledik egy \(\displaystyle M\) tömegű, \(\displaystyle R\) sugarú, gömb alakú bolygó felé (\(\displaystyle m\ll M\)). Az üstökös sebessége a bolygótól nagyon messze \(\displaystyle v_0\), és ha nem hatna rá a bolygó gravitációs tere, akkor \(\displaystyle d\) távolságra haladna el a bolygó középpontjától (\(\displaystyle d>R\)). Mekkora \(\displaystyle v_0\) minimális értéke, amelynél az üstökös még nem ütközik a bolygóba? (A bolygón és az üstökösön kívül minden más égitest gravitációs hatását elhanyagolhatjuk.)
Közli: Kovács József, Szombathely
(5 pont)
P. 5069. Egy \(\displaystyle \alpha\) hajlásszögű lejtőre \(\displaystyle M\) tömegű, \(\displaystyle R\) sugarú, tömör hengert helyeztünk, amit egy vízszintes kötél köt össze a lejtő tetejével az ábrán látható módon. A test mellett található még egy \(\displaystyle m\) tömegű, \(\displaystyle r\) sugarú tömör henger. A két henger közötti súrlódás elhanyagolható, és az \(\displaystyle M\) tömegű henger nem emelkedik meg. Legalább mekkora az \(\displaystyle R\) sugarú henger és a lejtő közötti tapadási súrlódási együttható, ha a hengerek nem csúsznak meg a lejtőn?
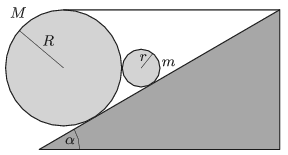
Adatok: \(\displaystyle \alpha=30^\circ\), \(\displaystyle R=3r\), \(\displaystyle M=3m\).
Közli: Takács Árpád, Budapest, Berzsenyi Dániel Gimnázium
(5 pont)
P. 5070. Egy \(\displaystyle \ell\) magasságú barlangban \(\displaystyle D\) rugóállandójú, feszítetlen állapotában \(\displaystyle d<\ell\) hosszúságú, elhanyagolható tömegű rugó helyezkedik el függőleges helyzetben. A rugó egyik végét a barlang mennyezetéhez, a másik végét pedig a talajhoz rögzítették az ábrán látható módon.

A rugó közepére rárepül és a rugóba kapaszkodik egy \(\displaystyle m\) tömegű, kis méretű denevér, és a rugó vezérelte bonyolult rezgésbe kezd. (A denevér mozgása során a rugó semelyik darabja nem lazul meg.)
\(\displaystyle a)\) Hol fog megállni a denevér a rezgés lecsillapodása után? (A rugó még nagy megnyújtásnál is követi a Hooke-törvényt.)
\(\displaystyle b)\) Innen a denevér igen óvatosan visszamászik újra a talajtól mért \(\displaystyle \ell/2\) magasságra. Legalább mekkora munkát végez eközben?
Közli: Balogh Péter, Gödöllő
(5 pont)
P. 5071. Rugalmas fonálon lógó terhet 0-ról lassan növekvő erővel húzunk lefelé. A fonál \(\displaystyle F_1\) erőnél szakad el. Milyen minimális erő alkalmazásánál szakad el a fonál, ha az erő azonnal felveszi értékét, és utána nem változik?
A Kvant nyomán
(5 pont)
P. 5072. A neonatom átmérője 0,32 nm. Adjunk becslést arra, hogy a neongáz normál állapotában
\(\displaystyle a)\) egyetlen atom átmérőjének átlagosan hányszorosa az atomok egymástól mért távolsága;
\(\displaystyle b)\) az atomok termikus átlagsebessége hányszorosa a gázban terjedő hang sebességének!
Közli: Radnai Gyula, Budapest
(4 pont)
P. 5073. Függőleges, igen hosszú (végtelennek vehető) egyenes szigetelőszál lineáris töltéssűrűsége \(\displaystyle \lambda= 8\cdot10^{-7}\) C/m. A száltól \(\displaystyle d_0=5\) cm távolságban igen vékony, \(\displaystyle \ell=10\) cm hosszú szigetelőfonálra felfüggesztünk egy \(\displaystyle m=2\) g tömegű, \(\displaystyle q=7\cdot10^{-8}\) C töltésű, kis méretű fémgolyót. A fonál függőleges állapotában a rögzítést lökésmentesen megszüntetjük.
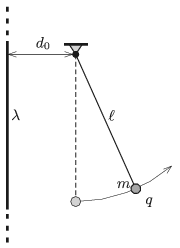
\(\displaystyle a)\) Milyen messzire távolodik el a fémgolyó a szigetelőszáltól?
\(\displaystyle b)\) Mekkora a fonál függőlegessel bezárt szöge, amikor a golyó sebessége maximális? Mekkora ez a maximális sebesség?
\(\displaystyle c)\) Mekkora erő hat a felfüggesztésre, amikor leggyorsabban mozog a golyó?
Közli: Holics László, Budapest
(5 pont)
P. 5074. Szabályos hatszög minden éle \(\displaystyle R\) ellenállású drótból áll. Az egyik csúcsból a nem szomszédos három másikba is mennek vezetékek átlósan, ugyanolyan drótból, mint amilyenből az oldalak állnak. Mekkora az eredő ellenállás ezen csúcs és a szemközti csúcs között?
Közli: Tornyos Tivadar Eörs, Budapest
(4 pont)
P. 5075. Az ábra szerinti elrendezésben közös optikai tengelyen, egymással párhuzamosan négy vékony lencse helyezkedik el. Mindegyik lencse határfelületének görbületi sugara 5 cm, illetve 10 cm. Kettő közülük \(\displaystyle n=1{,}5\) törésmutatójú üvegben lévő levegőlencse, kettő pedig ugyanilyen törésmutatójú üveglencse.
Az üvegben, az optikai tengelyen, a domborúan homorú lencsétől 60 cm-re egy pontszerű fényforrás van. A lencse másik oldalán, tőle 30 cm távolságra helyezkedik el a homorúan domború levegőlencse. Ettől 10 cm távolságra van az üveget határoló sík felület, amely merőleges az optikai tengelyre. A sík felülettől 10 cm-re található az üvegből készült domborúan homorú lencse, a negyedik (homorúan domború) lencse pedig a harmadiktól 20 cm-re van.
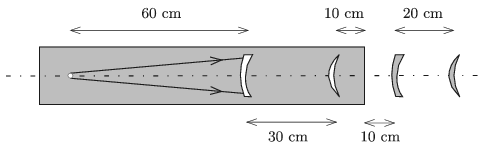
A négy lencse hová képezi le a pontszerű fényforrást?
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 5076. Egy optikai rácsot a résekre merőlegesen, de a rács síkjához képest ferdén, \(\displaystyle 45^\circ\)-os szögben világítunk meg monokromatikus, \(\displaystyle \lambda\) hullámhosszúságú lézerfénnyel. Határozzuk meg az elhajlási kép intenzitásmaximumainak számát és irányát, ha a rácsállandó
\(\displaystyle a)\) \(\displaystyle d=\lambda\);
\(\displaystyle b)\) \(\displaystyle d=5\lambda\).
Közli: Woynarovich Ferenc (Budapest)
(5 pont)
P. 5077. Egy téglatest alakú, hőszigetelő falú tartály közepén jó hővezető anyagból készült dugattyú helyezkedik el. A dugattyútól balra \(\displaystyle V_0\) térfogatú levegő van, a dugattyútól jobbra \(\displaystyle V_0/2\) térfogatú, \(\displaystyle p_0=76~{\rm Hgcm}\approx 10^5\) Pa nyomású levegő és \(\displaystyle h=38\) cm magas higanyoszlop található. A tartály teljes szélessége (a dugattyú vastagságán felül) \(\displaystyle 2h\), magassága szintén \(\displaystyle 2h\).
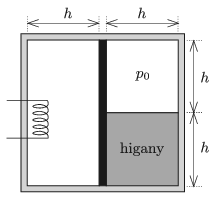
Egy beépített fűtőszállal lassan melegíteni kezdjük a bal oldali térrészt. A gázok hőmérséklete minden pillanatban megegyezik. Legfeljebb mekkora lehet a dugattyú elmozdulása, ha a higany, a tartály és a dugattyú hőtágulásától eltekintünk?
Közli: Berke Martin,
Zalaegerszegi Zrínyi Miklós Gimnázium
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

