A KöMaL 2018. decemberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2019. január 10-én LEJÁRT. |
K. 604. Adjunk meg öt különböző pozitív egész számot úgy, hogy közülük akárhányat kiválasztva és összeadva a számok összege minden választás esetén különböző legyen. Válasszuk meg ezt az öt számot úgy, hogy az öt szám közül a legnagyobb a lehető legkisebb legyen.
(6 pont)
K. 605. Kehelynek nevezünk három kiskockát, ha párosával egy-egy közös élük van (lásd az ábrát). Egységnyi élhosszúságú kiskockákból téglatesteket építettünk.
\(\displaystyle a)\) Hány kehely található egy \(\displaystyle 4\times4\times2\)-es téglatestben?
\(\displaystyle b)\) Hány kehely található egy \(\displaystyle 4\times4\times3\)-as téglatestben?
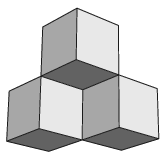
(6 pont)
K. 606. Egy \(\displaystyle ABCDE\) ötszög \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CD\) és \(\displaystyle DE\) oldala egységnyi hosszúságú, az \(\displaystyle ABC\sphericalangle\) és a \(\displaystyle CDE\sphericalangle\) is \(\displaystyle 90^{\circ}\)-os. Mutassuk meg, hogy ilyen ötszögekkel hézagmentesen parkettázható a sík. Mutassuk meg konvex és konkáv esetre is.
(6 pont)
K. 607. Egybevágó egyenlő oldalú háromszögekből szabályos hatszögeket építünk az ábrának megfelelően. Az első hat, a második huszonnégy háromszögből áll.
\(\displaystyle a)\) Hány háromszögből építhetjük meg a hatodik ilyen hatszöget?
\(\displaystyle b)\) 2017 háromszögünk van. Ezekből megépítjük a lehető legnagyobb szabályos hatszöget. Hány háromszögünk marad ki?

(6 pont)
K. 608. \(\displaystyle a)\) Mutassuk meg, hogy végtelen sok olyan egész szám van, melynek a négyzete három 4-esre végződik.
\(\displaystyle b)\) Van-e olyan egész szám, melynek a négyzete négy 4-esre végződik?
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2019. január 10-én LEJÁRT. |
C. 1511. Az \(\displaystyle AD\) szakasz \(\displaystyle B\) és \(\displaystyle C\) belső pontjaira \(\displaystyle AB=CD\) teljesül. Bizonyítsuk be, hogy ha \(\displaystyle P\) a sík egy tetszőleges pontja, akkor \(\displaystyle PA+PD\ge PB+PC\).
(5 pont)
C. 1512. Piros, fehér és zöld színű gyurma háromféle keverékéből 50 grammos kockákat készítünk. A színek aránya az első fajta kockában \(\displaystyle 3:2:0\), a másodikban \(\displaystyle 1:3:1\), a harmadikban pedig \(\displaystyle 0:1:4\). Melyik fajtából hány kockát készítsünk, ha mindegyik színből \(\displaystyle 1\) kg gyurmát szeretnénk felhasználni?
(5 pont)
C. 1513. Mutassuk meg, hogy bármely köbszám felírható két négyzetszám különbségeként.
(5 pont)
C. 1514. Az egységnégyzetet négy egyenlő szárú háromszögre bontjuk úgy, hogy a négyzet egy belső pontját összekötjük a csúcsokkal. Határozzuk meg a négy háromszög területe szorzatának minimális és maximális értékét.
(5 pont)
C. 1515. Oldjuk meg a következő egyenletet a valós számok halmazán, ha \(\displaystyle k\) páratlan pozitív egész szám:
\(\displaystyle \big(1-x+x^2\big) \big(1-x+x^2-\ldots +x^{2k}\big)= \big(1-x+x^2-\ldots +x^{k+1}\big)^2. \)
(5 pont)
C. 1516. Az \(\displaystyle O(4;-2)\) közepű, \(\displaystyle r=5\sqrt{3}\) sugarú körhöz érintőt húzunk a koordináta-rendszer \(\displaystyle P(16;7)\) pontjából. Az érintési pont merőleges vetületét az \(\displaystyle OP\) szakaszon jelölje \(\displaystyle P'\). Határozzuk meg \(\displaystyle P'\) koordinátáit.
(5 pont)
C. 1517. Egy sakktábla mezőit három színnel színeztük az ábrán látható módon. A táblán véletlenszerűen elhelyezünk egy huszárt, majd azzal véletlenszerűen (de szabályosan) egyet lépünk. Mekkora a valószínűsége annak, hogy a huszár a kiinduló mezővel azonos színű helyre érkezik?
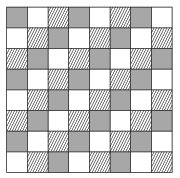
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2019. január 10-én LEJÁRT. |
B. 4990. Legyen \(\displaystyle n\) egynél nagyobb természetes szám. Jelölje \(\displaystyle n\) pozitív osztóinak számát \(\displaystyle d(n)\), összegét pedig \(\displaystyle \sigma(n)\). Mutassuk meg, hogy
\(\displaystyle \sigma(n) > d(n)\sqrt n\,. \)
Javasolta: Sárosdi Zsombor (Veresegyház)
(3 pont)
B. 4991. Artúr és Blanka egy kocka éleit felváltva pirosra festik úgy, hogy minden lépésben olyan élt színeznek ki, amely kitérő az utolsó lépésben kifestett élhez. A színezést Artúr kezdi. Az veszít, aki nem tud lépni. Kinek van nyerő stratégiája?
(3 pont)
B. 4992. Az \(\displaystyle 1,2,\ldots, n\) számok mindegyikét pirosra vagy kékre színezzük. Egy lépés azt jelenti, hogy kiválasztunk három különböző számot, amelyek számtani sorozatot alkotnak, és mindhárom szám színét a másik színre változtatjuk. Mely \(\displaystyle n\)-ekre lehet az \(\displaystyle 1,2,\ldots, n\) számok tetszőleges színezéséből kiindulva elérni, hogy mindegyik szám piros legyen?
Javasolta: Róka Sándor (Nyíregyháza)
(4 pont)
B. 4993. Rajzoljunk az \(\displaystyle ABC\) derékszögű háromszög \(\displaystyle BC\) és \(\displaystyle CA\) befogói fölé négyzeteket. A négyzetek \(\displaystyle C\)-vel átellenes csúcsai legyenek \(\displaystyle D\) és \(\displaystyle E\). Mutassuk meg, hogy az \(\displaystyle ABC\) háromszög köré írt kör átmegy a \(\displaystyle DE\) szakasz felezőpontján.
(4 pont)
B. 4994. Bizonyítsuk be, hogy ha \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) olyan valós számok, amelyekre az \(\displaystyle x^3+Ax^2+Bx+C=0\) paraméteres harmadfokú egyenletnek három különböző pozitív gyöke van, akkor \(\displaystyle A^2+B^2+18C>0\).
(Német feladat)
(4 pont)
B. 4995. Legyenek az \(\displaystyle ABC\) hegyesszögű, nem egyenlő szárú háromszög \(\displaystyle BC\), \(\displaystyle CA\) és \(\displaystyle AB\) oldalainak felezőpontjai rendre \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle F\), a háromszög körülírt körének középpontja \(\displaystyle O\), magasságpontja \(\displaystyle M\). Az \(\displaystyle ABC\) háromszög körülírt köréhez az \(\displaystyle A\) pontban húzott érintő és az \(\displaystyle EF\) egyenes metszéspontja \(\displaystyle P\), a körülírt körhöz a \(\displaystyle B\) pontban húzott érintő és \(\displaystyle FD\) metszéspontja \(\displaystyle Q\). Mutassuk meg, hogy a \(\displaystyle PQ\) egyenes merőleges az \(\displaystyle OM\) egyenesre.
Javasolta: Bíró Bálint (Eger)
(5 pont)
B. 4996. Adott egy szakasz és az egyik harmadolópontja. Szerkesszük meg csak vonalzó segítségével a másik harmadolópontot.
(6 pont)
B. 4997. Tekintsük egész együtthatós polinomok következő \(\displaystyle p_n(x)\) sorozatát: legyen \(\displaystyle p_0(x)=0\), \(\displaystyle p_1(x)=1\), és minden \(\displaystyle n\ge 2\) esetén
\(\displaystyle p_n(x)=p_{n-1}(x)+x\cdot p_{n-2}(x). \)
Bizonyítsuk be, hogy ha valamilyen \(\displaystyle n\), \(\displaystyle m\) pozitív egészekre egy \(\displaystyle f(x)\) polinom osztója a \(\displaystyle p_n(x)\) és \(\displaystyle p_m(x)\) polinomnak, akkor a \(\displaystyle p_{(m,n)}(x)\) polinomnak is osztója.
(\(\displaystyle (n,m)\) jelöli az \(\displaystyle n\) és \(\displaystyle m\) legnagyobb közös osztóját. A \(\displaystyle P(x)\) polinom osztója a \(\displaystyle Q(x)\) polinomnak, ha van olyan \(\displaystyle R(x)\) valós együtthatós polinom, amelyre \(\displaystyle Q(x)= P(x)R(x)\).)
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2019. január 10-én LEJÁRT. |
A. 737. Adott \(\displaystyle 100\) pont a térben úgy, hogy közülük semelyik négy nem esik egy síkba. Tekintsük azokat az öt csúcsú konvex poliédereket, amelyeknek minden csúcsa az adott halmazból való. Igazoljuk, hogy az ilyen poliéderek száma páros.
Javasolta: Károlyi Gyula (Budajenő)
(7 pont)
A. 738. (A decemberben kitűzött feladatunk hibás volt. Új feladatot tűzünk ki helyette, amely a januári feladatokkal együtt küldhető be.)
Tekintsük a következő számsorozatot: \(\displaystyle a_1=1\), \(\displaystyle a_2=2\), \(\displaystyle a_3=3\), illetve
\(\displaystyle a_{n+3}=\frac{a_{n+1}^2+a_{n+2}^2-2}{a_n}\)
minden \(\displaystyle n\ge 1\) egészre. Bizonyítsuk be, hogy a sorozat minden tagja pozitív egész szám.
(7 pont)
A. 739. Legyen \(\displaystyle a_1,a_2,\ldots\) a \(\displaystyle [0,1]\) intervallumba eső valós számok egy sorozata. Bizonyítsuk be, hogy van pozitív egészeknek olyan \(\displaystyle 1\le n_1<n_2<\ldots\) sorozata, amelyre
\(\displaystyle A=\lim_{\substack{i, j\to \infty\\i\ne j}} a_{n_i+n_j} \)
létezik, azaz minden \(\displaystyle \varepsilon>0\) számhoz van olyan \(\displaystyle N_\varepsilon\), hogy \(\displaystyle \big|a_{n_i+n_j}-A\big| < \varepsilon\) teljesül bármely, egymástól különböző \(\displaystyle i,j>N_\varepsilon\) indexek esetén.
CIIM 10, Kolumbia
(7 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
