A KöMaL 2020. januári fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2020. február 10-én LEJÁRT. |
M. 392. Mérjük meg a 100 forintos vagy az 1 eurós pénzérme anyagának fajhőjét kaloriméterben (termoszban)!
Közli: Gnädig Péter, Vácduka
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2020. február 10-én LEJÁRT. |
G. 693. Két teljesen hasonló vonat két párhuzamos vágányon halad egymással szemben állandó (de nem feltétlenül azonos nagyságú) sebességgel. A mozdonyok ugyanolyan hosszúságúak, mint a kocsik. Mindkét vonat 19 kocsiból és a mozdonyból áll, amely vontatja a szerelvényt. Az egyik vonaton Piri elölről a harmadik kocsiban utazik. Miután a két vonat találkozik, Piri kocsija 36 másodperc múlva kerül teljes terjedelmében Dani szemből jövő kocsija mellé, és ezt követően újabb 44 másodperc telik el, amíg a két vonat teljesen elhalad egymás mellett. Elölről hányadik kocsiban utazik Dani?
Közli: Székely Zoltán, Székelyudvarhely
(4 pont)
G. 694. Egy éppen 100 kg tömegű rakéta a világűrben másodpercenként 100 g égésterméket lövell ki. A gáz 1 km/s sebességgel hagyja el a rakéta fúvókáját. Mekkora a rakéta gyorsulása?
(3 pont)
G. 695. Játékpingvineket függesztettek egy mozgó szobadíszre. A nagyon könnyű rudakat a negyedelőpontjukban függesztették fel, és így egyensúlyban vannak. Mekkora a 2., a 3. és a 4. pingvin tömege, ha tudjuk, hogy az első 48 dkg tömegű?
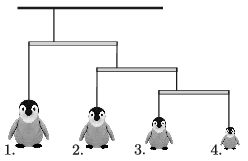
Amerikai feladat
(3 pont)
G. 696. Sanyi egy forrasztópákát kapott karácsonyra, és rögtön kipróbálta. Egy \(\displaystyle 2000~\Omega\)-os ellenállással párhuzamosan összeforrasztott egy \(\displaystyle 500~\Omega\)-os ellenállást, majd az egésszel sorba egy másik \(\displaystyle 500~\Omega\)-osat, végül az így kapott elrendezéssel párhuzamosan egy \(\displaystyle 600~\Omega\)-os ellenállást. Az egészet egy telepre kapcsolta, és megállapította, hogy így a \(\displaystyle 2000~\Omega\)-os ellenálláson 2 V feszültség mérhető.
\(\displaystyle a)\) Készítsük el az áramkör kapcsolási rajzát!
\(\displaystyle b)\) Mekkora a telep feszültsége?
\(\displaystyle c)\) Mekkora a telepen átfolyó áram erőssége?
(3 pont)
 |
P-jelű feladatokA beküldési határidő 2020. február 10-én LEJÁRT. |
P. 5186. Egy szánkó és a rajta ülő gyerek együttes tömege 25 kg. A csúszási súrlódási tényező a hóban 0,05.
\(\displaystyle a)\) Szeretnénk vízszintes terepen állandó sebességgel húzni a szánkót. Mekkora vízszintes erő szükséges ehhez?
\(\displaystyle b)\) A szánkót vízszintes, havas talajon 2 másodpercen át 50 N erővel felgyorsítjuk álló helyzetből, majd magára hagyjuk. Mekkora utat tesz meg a szánkó az indulás és a megállás között?
Tarján Imre emlékverseny (Szolnok) feladata alapján
(3 pont)
P. 5187. Egy \(\displaystyle \ell_1=25~\)cm és egy \(\displaystyle \ell_2=1{,}2\) m hosszú fonálingát azonos magasságban rögzítünk. A lengések síkja párhuzamos, és egymáshoz elég közel van. Az ingákat az egyensúlyi helyzetből azonos nagyságú, kis szöggel, ellentétes irányban kitérítjük, majd elengedjük.
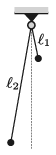
\(\displaystyle a)\) Az induláshoz képest mennyi idő múlva halad el egymás mellett a két fonálinga?
\(\displaystyle b)\) Mennyi idő múlva találkoznak másodszor?
\(\displaystyle c)\) Mekkorára kellene változtatni az ingahosszak arányát, hogy az ötödik találkozás legyen az első olyan, amikor az ingák sebességének iránya azonos?
Közli: Zsigri Ferenc, Budapest
(5 pont)
P. 5188. Vízszintes felületen egyenes vonalban mozgó, téglatest alakú hasáb a súrlódás következtében egyenletesen lassul. Az ábra a hasáb mozgásának sebesség–idő grafikonját mutatja.
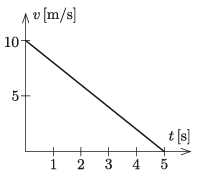
A hasáb tetejére rugós játékágyút rögzítettek, ami \(\displaystyle v_0\) torkolati sebességű, \(\displaystyle m\) tömegű lövedéket lő ki pillanatszerűen a hasáb lassuló mozgása során. A hasáb és az ágyú együttes tömege \(\displaystyle M\).
\(\displaystyle a)\) Milyen irányban álljon az ágyú csöve, hogy a kilövés egyáltalán ne legyen hatással a hasáb lassulására, vagyis a grafikon az ábra szerint folytatódjon a kilövés után is?
\(\displaystyle b)\) Ha az ágyúcsövet az előzőekben meghatározott szög felére engedjük le, akkor a kilövés milyen módon befolyásolja a lassulási grafikont? Ábrázoljuk a módosult sebesség-idő grafikont, ha a kilövés \(\displaystyle t=2\) s-nál következik be!
Adatok: \(\displaystyle m=0{,}1~\)kg, \(\displaystyle M=1~\)kg, \(\displaystyle v_0=5~\)m/s.
Közli: Honyek Gyula, Veresegyház
(5 pont)
P. 5189. Hosszú, hengeres, glicerinnel teli cső közepében kicsiny légbuborék van. Ha a csövet függőlegesen felállítjuk, a buborék állandó, 1 cm/s nagyságú sebességgel emelkedik. Ha a cső vízszintes, és a tengelyével párhuzamosan 20 m/s sebességre gyorsítják, hol áll meg a csőben a buborék? Hová mozdul el a buborék, ha a cső sebességét egyenletesen 30 m/s-ra növelik? És hol áll meg ezután, ha a csövet lefékezik? (A buborék megindulásának és megállásának rövid időtartamát, valamint a cső falának fékező hatását hanyagoljuk el.)
A Kvant nyomán
(5 pont)
P. 5190. Egy vékony falú, függőlegesen álló üvegcső alul szabályos félgömb alakú. A cső átmérője 10 cm. Vizet töltünk a csőbe, 20 cm magasan. A cső tengelye mentén, a vízfelület felett 30 cm magasan egy kicsiny fényforrás világít.
\(\displaystyle a)\) Hova tegyünk egy ernyőt, hogy azon a fényforrás éles képe jelenjen meg?
\(\displaystyle b)\) Mekkora a kép nagyítása?
(A víz törésmutatója \(\displaystyle n= 4/3\).)
Közli: Radnai Gyula, Budapest
(5 pont)
P. 5191. Ugyanannyi ideális gázzal az ábra szerinti \(\displaystyle p\,\)–\(\displaystyle \,V\) diagramon ábrázolt \(\displaystyle 1\rightarrow2\rightarrow3\rightarrow1\), illetve az \(\displaystyle 1\rightarrow3\rightarrow4\rightarrow1\) körfolyamatot végeztetjük. Melyik körfolyamatot végző gépnek nagyobb a hatásfoka, és milyen összefüggés áll fenn a két hatásfok között?
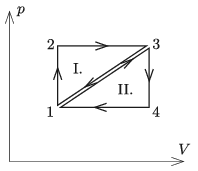
Varga István (1952–2007) feladata
(5 pont)
P. 5192. Az ábrán látható, egyik végén zárt, U alakú, \(\displaystyle 1~\mathrm{cm}^2\) keresztmetszetű csőben lévő higany \(\displaystyle 40\) cm hosszúságú, 300 K hőmérsékletű levegőt zár be. A külső légnyomás 76 cm magas higanyoszlop hidrosztatikai nyomásával egyezik meg.
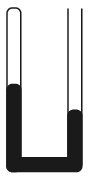
A bezárt gáz hőmérsékletét állandónak tartva, \(\displaystyle V_0\) térfogatú higany betöltése után a cső két szárában a higanyszint megegyezik. Ha ezek után a bezárt levegőt melegítjük, azt tapasztaljuk, hogy a nyomása minden hőmérsékleten egyenesen arányos a térfogatával. Mekkora a \(\displaystyle V_0\) térfogat?
Közli: Kotek László, Pécs
(5 pont)
P. 5193. Hat darab ohmos ellenállást az ábrán látható módon forrasztottunk össze. Mekkora eredő ellenállás mérhető a \(\displaystyle 20~\Omega\)-os ellenállás végpontjai között?
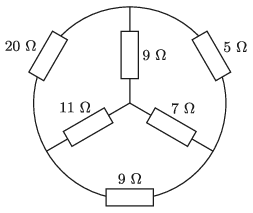
(Lásd A hídkapcsolás eredő ellenállása és áramerősségei című cikket a KöMaL 2016. évi 2. számában vagy a honlapon.)
Közli: Légrádi Imre, Sopron
(4 pont)
P. 5194. Tekintsünk két azonos méretű, de a köztük lévő 0,2 m távolsághoz képest kicsiny fémgömböt! A két gömbnek különböző töltése van, és 1,2 N erővel vonzzák egymást. A gömböket összeérintjük, majd visszahelyezzük őket az eredeti helyükre. Azt találjuk, hogy most taszítják egymást, de az erő nagysága az előzővel azonos. Mennyi volt a fémgömbök eredeti töltése?
Tornyai Sándor fizikaverseny, Hódmezővásárhely
(4 pont)
P. 5195. Egy \(\displaystyle a=60~\)cm oldalhosszúságú, egyenlő oldalú háromszög csúcsaiban egy-egy \(\displaystyle Q=6\cdot 10^{-7}\) C nagyságú, pontszerűnek tekinthető töltés helyezkedik el vákuumban. Mekkora és milyen irányú az elektromos térerősség a háromszög oldalharmadoló pontjaiban?
Közli: Holics László, Budapest
(4 pont)
P. 5196. Egy rakéta a hajtóművének működése közben csak a kiáramló gázsugárra ,,támaszkodhat''. A hajtóanyag energiájának jelentős részét a kiáramló gázok viszik magukkal, a rakéta mozgási energiájának növelésére a felszabaduló energia kisebb hányada jut.
\(\displaystyle a)\) Határozzuk meg, hogy mekkora \(\displaystyle \Delta v\) értékkel nő a rakéta sebessége, ha az \(\displaystyle M\) tömegű rakétából valamennyi idő alatt egy kicsiny \(\displaystyle \Delta M\) tömegű gáz áramlik ki hátrafelé, a rakétához képest \(\displaystyle u\) sebességgel! (A gravitációs erőt itt és a továbbiakban elhanyagoljuk.)
\(\displaystyle b)\) Mekkora lesz az \(\displaystyle M_0\) tömeggel induló rakéta sebessége, amikor a tömege már \(\displaystyle M\) \(\displaystyle (M<M_0)\) értékre csökken?
Útmutatás: felhasználhatjuk, hogy
\(\displaystyle \int_{x_1}^{x_2} \frac{1}{x}\, \mathrm{d}x=\ln \frac{x_2}{x_1}. \)
\(\displaystyle c)\) Mekkora az \(\displaystyle M\) tömegű rakéta és a kiáramlott gázok összes mozgási energiája az indulási vonatkoztatási rendszerben?
Útmutatás: felhasználhatjuk, hogy a kiáramlott gázokból és a rakétából álló teljes rendszer mozgási energiájának megváltozása független a vonatkoztatási rendszertől, így pl. a rakétával együtt mozgó rendszerben is ugyanakkora, mint az indulási vonatkoztatási rendszerben.
\(\displaystyle d)\) Legfeljebb mekkora lehet a rakétameghajtás ,,mechanikai hatásfoka'', vagyis a rakéta mozgási energiájának és az összes mozgási energiának a hányadosa az indítási vonatkoztatási rendszerben?
Némedi István (1932–1998) feladata
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

