A KöMaL 2023. januári fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2023. február 15-én LEJÁRT. |
M. 419. Vágjunk ki A4-es fénymásolópapírból kb. 2 cm szélességű csíkokat a papírlap hosszabb, illetve a rövidebb oldalaival párhuzamosan. A papírcsíkok középső harmadát az ábrának megfelelően, ívelt vonalak mentén keskenyítsük el! Mérjük meg ezek használatával a papír (MPa egységekben kifejezett) szakítószilárdságát! Van-e eltérés a hosszabb, illetve a rövidebb irányban kivágott csíkok szakítószilárdsága között?
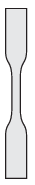
Közli: Gnädig Péter, Vácduka
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2023. február 15-én LEJÁRT. |
G. 801. Vízszintes talajon két, síléceken álló, 72 kg tömegű férfi közül az első 0,02 bar, míg a második 0,025 bar nyomást gyakorol a hóra. A második férfi 5 kg tömegű hátizsákot is visel a hátán.
\(\displaystyle a)\) Mekkora a sílécek nyomófelülete?
\(\displaystyle b)\) Mekkora lesz a második férfi alatt a nyomás, ha hátizsákját ledobja és féllábra áll?
(3 pont)
G. 802. Körülbelül hány perccel később delel a Nap Sopronban, mint Mátészalkán?
Közli: Németh László, Fonyód
(3 pont)
G. 803. Egyenes mentén állandó lassulással haladó test egy pályaszakasz végére érve elveszíti kezdősebességének a felét. Kezdősebességének hány százalékát vesztette el a pályaszakasz felezőpontjáig?
(4 pont)
G. 804. Egy \(\displaystyle 0{,}6~\mathrm{kg/dm}^3\) sűrűségű fahasáb, melynek magassága 40 cm, alapélei pedig 80 cm és 30 cm hosszúak, egy nagy méretű medencében úszik. A hasábot az ábrán látható módon a medence aljához rögzítettük egy rugóval, melynek nyújtatlan hossza 50 cm.
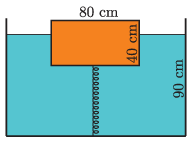
\(\displaystyle a)\) Mennyi látszik ki a hasábból, ha víz mélysége 90 cm és a rugó rugóállandója 1440 N/m?
\(\displaystyle b)\) Legalább mekkora munkavégzés árán lehet a hasábot teljesen a víz felszíne fölé emelni, ha a rugó közben nem szakad el?
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2023. február 15-én LEJÁRT. |
P. 5454. Az autógumik javítása után a kerekeket nagy fordulatszámra pörgetik, és az esetleges ,,ütést'' kicsiny nehezékekkel kiegyensúlyozzák (centrírozzák a kereket). Az egyik kereket álló helyzetből állandó szöggyorsulással forgásba hozzák. Egy bizonyos pillanatban a tengelytől \(\displaystyle R=20\) cm távolságban lévő szelepsapka gyorsulásának nagysága kétszer akkora, mint az induláskor, és a sebessége ekkor \(\displaystyle v=1\) m/s.
\(\displaystyle a)\) Mennyi idő telt el az indulásától számítva?
\(\displaystyle b)\) Mennyi volt a szelepsapka gyorsulása induláskor?
\(\displaystyle c)\) Mennyi utat tett meg a szelepsapka ezalatt?
Közli: Holics László, Budapest
(4 pont)
P. 5455. Egy függőleges tengelyű, \(\displaystyle 45^\circ\)-os félnyílásszögű, súrlódásmentes tölcsér belső felületére, a tengelyétől 10 cm távolságban \(\displaystyle v_0\) nagyságú vízszintes sebességgel egy pontszerű testet juttatunk. Mekkora lesz a test legnagyobb sebessége, ha
\(\displaystyle a)\) \(\displaystyle v_0= 0{,}5\) m/s;
\(\displaystyle b)\) \(\displaystyle v_0= 2{,}0\) m/s?
Példatári feladat nyomán
(5 pont)
P. 5456. A képen azt láthatjuk, hogy munkások egy kútgyűrűt raknak fel (vagy esetleg engednek le) pallókon egy teherautóról. A kútgyűrű tömege 300 kg, átmérője 1 m, a pallók hossza 5 m, a teherautó platójának magassága 1 m. Tegyük fel, hogy a munkások kezei által kifejtett erők eredője párhuzamos a pallókkal, valamint a kezük és a kútgyűrű között 0,8 a tapadási súrlódási együttható, továbbá a kútgyűrű nem csúszik meg a pallón.

Határozzuk meg, hogy a pallókkal párhuzamosan legalább mekkora erőt kell a betongyűrűre kifejteni, ha egyenletes mozgással, megcsúszás nélkül akarjuk görgetni
\(\displaystyle a)\) felfelé;
\(\displaystyle b)\) lefelé!
Közli: Honyek Gyula, Veresegyház
(5 pont)
P. 5457. Hőszigetelt, hengeres tartály belső hossza \(\displaystyle L\). A tartályt egy hőszigetelő dugattyú két részre osztja; a bal oldali térfélben egyatomos ideális gáz, a jobb oldaliban vákuum van (lásd az ábrát). A dugattyút a tartály jobb oldali végével rugó köti össze, melynek feszítetlen hossza \(\displaystyle L\). A gázt a bal oldali térfélben lévő fűtőszál segítségével lassan melegíteni kezdjük.
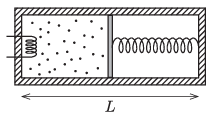
Határozzuk meg a gáz mólhőjét ebben a folyamatban!
Oroszországi feladat nyomán
(5 pont)
P. 5458. Három telep mindegyike 12 V üresjárási feszültségű és \(\displaystyle 3~\Omega\) belső ellenállású. A telepek milyen kapcsolása esetén kapjuk az \(\displaystyle R\) külső ellenálláson a legnagyobb teljesítményt, és mekkora ez a teljesítmény, ha
\(\displaystyle a)\) \(\displaystyle R = 1~\Omega\);
\(\displaystyle b)\) \(\displaystyle R = 3~\Omega\);
\(\displaystyle c)\) \(\displaystyle R = 3{,}5~\Omega\);
\(\displaystyle d)\) \(\displaystyle R = 6~\Omega\)?
Közli: Székely György, Budapest
(4 pont)
P. 5459. Egyenletes vastagságú ellenálláshuzalból \(\displaystyle R\) sugarú kört hajlítunk. A kör egyik pontjánál ,,sugárirányban'' \(\displaystyle I\) erősségű áramot vezetünk be, egy másik pontjánál pedig (ugyancsak sugárirányban) elvezetjük azt.
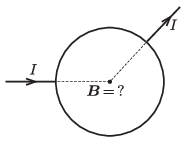
Milyen irányú és mekkora nagyságú a mágneses indukcióvektor a kör középpontjában?
Közli: Cserti József, Budapest
(3 pont)
P. 5460. Színes parfümöt 4 cm külső átmérőjű, 10 cm magas, állandó falvastagságú, henger alakú, \(\displaystyle n=1{,}5\) törésmutatójú üvegben hoznak forgalomba. A parfümöt a polcon szemmagasságban helyezik el, és hátulról világítják meg. A távoli vásárlók úgy látják, mintha a hengerpalást falvastagsága nulla lenne (a fénykép csak illusztráció, az üveg alakja és a falvastagsága eltér a feladatban leírtaktól). Legalább hány ml parfüm lehet az üvegben?

Közli: Széchenyi Gábor, Budapest
(4 pont)
P. 5461. A \(\displaystyle {}^{40}\mathrm{K}\) izotóp más elem bomlása közben nem jön létre, így a mennyisége a Föld létrejötte óta 1,25 milliárd évenként feleződik. A \(\displaystyle {}^{40}\mathrm{K}\) 11%-ban elektronbefogással (EB) vagy \(\displaystyle \beta^+\)-bomlással, 89%-ban \(\displaystyle \beta^{-}\)-bomlással alakul át.
\(\displaystyle a)\) Milyen magok keletkeznek az egyes radioaktív folyamatokban?
\(\displaystyle b)\) Az egyik bomlástermék gáz halmazállapotú, amely egy adott kőzet megszilárdulása után már nem jut ki abból. Ezt a kőzetmintát analizálva azt tapasztaljuk, hogy a keletkezett gáz anyagmennyisége 90%-a volt a még meglevő \(\displaystyle {}^{40}\mathrm{K}\)-nak. Mennyi idővel ezelőtt szilárdult meg a kőzet?
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 5462. Elhanyagolható tömegű rugóhoz hosszú hasábot erősítünk. Ha a rugót a másik végénél fogva felfüggesztjük, megnyúlása \(\displaystyle s=15\) cm lesz. Ezután a rugót és a hasábot vízszintes, súrlódásmentes síkra helyezzük, és a rugó szabad végét rögzítjük. A hasábot az ábrán látható módon \(\displaystyle \ell\) távolsággal hátrahúzzuk, így a rugó megnyúlik. Végül a hasáb felső lapjára, annak rugó felőli végére egy kocka alakú testet helyezünk. A hasáb és a kocka közötti (tapadási és csúszási) súrlódási együttható \(\displaystyle \mu=0{,}2\).
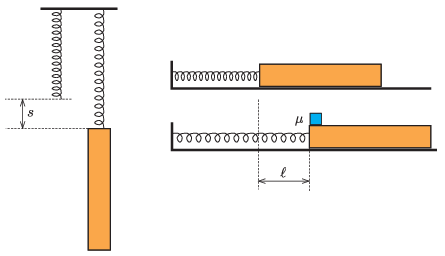
Ha a hasábot elengedjük, a rendszer mozgásba jön, és a kocka elcsúszik a hasábon. A két test közötti csúszás azt a pillanatot követően szűnik meg, amikor a hasáb gyorsulása nullává válik.
\(\displaystyle a)\) Mennyi ideig csúszott a kocka a hasábon?
\(\displaystyle b)\) Legalább mekkora az \(\displaystyle \ell\) távolság, ha a leírt mozgás létrejöhetett?
\(\displaystyle c)\) Mekkora távolsággal csúszott el a kocka a hasábon?
Közli:Wiedemann László, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

