| [397] Ármós Lajos | 2025-09-24 20:39:43 |
 A 2023/2-es feladatot az idők folyamán többször is nézegettem, de túl sok volt a mindenféle összefüggés, így kissé elvesztem benne. Most megcsináltam, sőt azt a sokféle összefüggést egy új feladatként meg is mutatnám.
Az eredeti feladat:
Legyen ABC egy hegyesszögű háromszög, amelyben AB < AC. Jelölje ABC körülírt körét Ω, melyen legyen S (az A pontot tartalmazó) CB ív felezőpontja. Az A pontból BC-re bocsátott merőleges a BS egyenest D-ben, az Ω kört pedig az E ≠ A pontban metszi. Továbbá a BC-vel párhuzamos, D ponton átmenő egyenes az L pontban metszi a BE egyenest. Jelölje a BDL háromszög körülírt körét ω, és legyen P az ω és Ω körök B-től különböző metszéspontja.
Bizonyítsuk be, hogy az ω-hoz P-ben húzott érintő és a BS egyenes a BAC∢ belső szögfelezőjén metszik egymást.
Ennek folytatásaként lássuk be a következőket:
Legyen Z az AD egyenesnek az ω körrel alkotott D-től különböző metszéspontja.
Bizonyítsuk be, hogy az LD, PC, SE és BZ egyenesek egy pontban metszik egymást.
Az eredeti és az új feladat megoldása: https://tinyurl.com/25zb8zdx
|
|
|
|
| [394] Lpont | 2025-08-17 19:13:27 |
 Szép megoldás a Tiéd is és Kós Gézáé is. Az enyém kevésbé elegáns.
Érdemes az alábbi oldalt is tanulmányozni - ha esetleg nem ismered -, remek feladatok megoldásokkal, köztük fogós geometriai problémák.
https://calimath.org/problems-solutions
|
| Előzmény: [393] Ármós Lajos, 2025-08-05 17:10:18 |
|
| [393] Ármós Lajos | 2025-08-05 17:10:18 |
 Tetszetős megoldás. Mivel nagyon sok összefüggés (szögegyenlőségek, párhuzamosságok) találhatóak a feladat felfejtése során, így vélelmezhető, hogy sokféle úton el lehet jutni a megoldáshoz. Mindenképpen egy érdekes, élvezetes geometriai feladat volt.
|
| Előzmény: [392] Kós Géza, 2025-08-04 12:39:59 |
|
| [392] Kós Géza | 2025-08-04 12:39:59 |
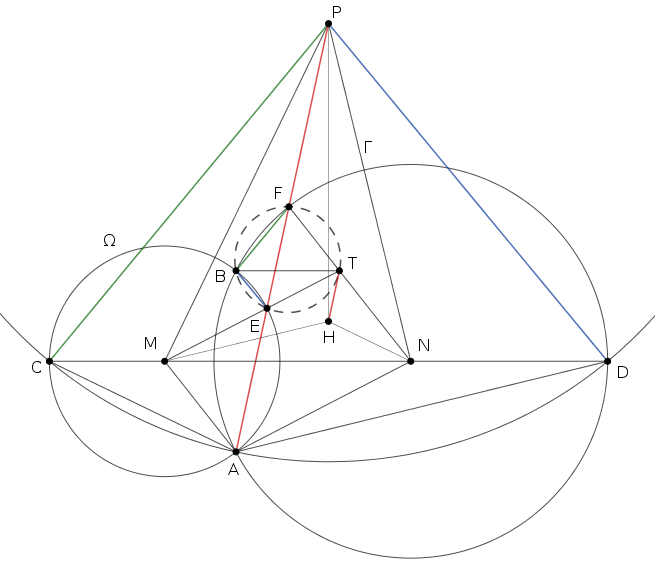
 Sok minden közös az én megoldásommal, én is használtam azt, hogy \(\displaystyle M,E,X\), illetve \(\displaystyle N,F,X\) egy egyenesen van, \(\displaystyle H\) az \(\displaystyle MNX\) háromszögbe írt kör középpontja, de nem használtam a \(\displaystyle Q,R\) pontokat.
Legyen \(\displaystyle T\) az \(\displaystyle ME\) és \(\displaystyle NF\) egyenes metszéspontja. (\(\displaystyle T\), mint "tangent", inkább nem módosítanám az ábrát; a piszkozat papírból tudjuk vagy egy jó ábrából sejtjük, hogy \(\displaystyle M,E,T\), illetve \(\displaystyle N,F,T\) egy egyenesen lesz, praktikus inkább így definiálni a pontot.) Megmutatjuk, hogy
(1) az \(\displaystyle BFE\) kör átmegy a \(\displaystyle T\) ponton;
(2) \(\displaystyle TH\) párhuzamos \(\displaystyle AP\)-vel;
(3) \(\displaystyle TH\) érinti a \(\displaystyle BFE\) kört.
\(\displaystyle PC\parallel FB\) és hasonlóan \(\displaystyle PD\parallel BE\), mert \(\displaystyle {CPA}\sphericalangle =2{CDA\sphericalangle} ={BDA\sphericalangle} ={BFA\sphericalangle}\).
Az \(\displaystyle EFT\triangle\) egyenlő szárú, és \(\displaystyle EFT\triangle\sim DCP\triangle\), mert \(\displaystyle {EFT\sphericalangle} ={NAP\sphericalangle} ={PDN\sphericalangle} ={MCP\sphericalangle} ={PAM\sphericalangle} ={MEA\sphericalangle} ={TEF\sphericalangle}\).
A \(\displaystyle B,F,T,E\) pontok egy körön vannak, mert \(\displaystyle {FTE\sphericalangle} = {CPD\sphericalangle} =180^\circ-{EBF\sphericalangle}\).
A \(\displaystyle BFTE\) körben \(\displaystyle BT\) felezi az \(\displaystyle {EBF}\) szöget. A \(\displaystyle CDP\) egyenlő szárú háromszögben a \(\displaystyle CD\) alap párhuzamos \(\displaystyle {CPD\sphericalangle}\) külső szögfelezőjével, így tehát \(\displaystyle BT\parallel CD\).
\(\displaystyle CPH\sphericalangle = \frac{1}{2} CPD\sphericalangle = \frac{1}{2} (CPA\sphericalangle + APD\sphericalangle) = MPA\sphericalangle + APN\sphericalangle = MPN\sphericalangle\), miatt \(\displaystyle CPM\sphericalangle = HPN\sphericalangle\), így
\(\displaystyle {NMT\sphericalangle} ={BTM\sphericalangle} ={BFE\sphericalangle} ={CPA\sphericalangle} =2{CPM\sphericalangle} =2{HPN\sphericalangle}
\stackrel{\text{merőleges szárú szögek}}{=}
2{NMH\sphericalangle},\)
tehát \(\displaystyle MH\) felezi az \(\displaystyle {NMT}\) szöget. Hasonlóan, \(\displaystyle NH\) felezi a \(\displaystyle {TNM}\) szöget.
Ezek után \(\displaystyle H\) az \(\displaystyle {MTN}\) háromszögbe írt kör középpontja, és \(\displaystyle TH\) felezi az \(\displaystyle {MTN}\) szöget, tehát \(\displaystyle TH\) az \(\displaystyle FTE\) szög külső felezője. Ezért az \(\displaystyle EFT\) egyenlő szárú háromszögben a \(\displaystyle TH\parallel AEFP\) és \(\displaystyle TH\) érinti az \(\displaystyle EFT\) kört.
|
 |
| Előzmény: [391] Ármós Lajos, 2025-08-03 11:15:03 |
|
|
|
|
| [388] Ármós Lajos | 2025-07-19 16:54:18 |
 Véget ért a 2025-ös Nemzetközi Matematikai Diákolimpia. A magyar csapat a 14. lett, 2 arany-, 3 ezüst- és egy bronzérmet nyertünk. További részletek: https://www.imo-official.org/results.aspx
|
|
|
| [385] Lpont | 2024-09-05 21:21:07 |
 Írtad, hogy érdekel a geometria, javaslom az idei MEMO egyéni és csapatversenyének összesen három geometria feladatát.
https://memo2024.bolyai.hu/competition/problems-solutions
|
| Előzmény: [383] Ármós Lajos, 2024-07-25 08:01:00 |
|
|
| [383] Ármós Lajos | 2024-07-25 08:01:00 |
 Én a geometriai feladatokat szoktam nézegetni, most csak egy volt belőle, az is jóval könnyebb volt szerintem a szokásostól. Itt egy megoldás rá Geogebrában: https://www.geogebra.org/geometry/tbgjyzry (Az alsó sávban lévő nyilakkal lehet lépésenként végigkövetni az elejétől a feladatot és a megoldását.)
|
|
|
|
| [380] Sinobi | 2024-07-24 20:27:21 |
 2-es és 3-as feladat még egyszer.
2. feladat Határozzuk meg az összes, pozitív egészekből álló \(\displaystyle (a, b)\) számpárt, melyre léteznek \(\displaystyle g\) és \(\displaystyle N\) pozitív egészek úgy, hogy
\(\displaystyle
\text{lnko(}a^{n}+b, b^{n}+a\text{)}=g \)
teljesül minden \(\displaystyle n \geq N\) egészre. (Az \(\displaystyle x\) és \(\displaystyle y\) egész számok legnagyobb közös osztóját lnko\(\displaystyle (x, y)\) jelöli.)
3. feladat Legyen \(\displaystyle a_{1}, a_{2}, a_{3}, \ldots\) pozitív egészek egy végtelen sorozata, valamint legyen \(\displaystyle N\) egy pozitív egész. Tegyük fel, hogy minden \(\displaystyle n>N\) esetén \(\displaystyle a_{n}\) megegyezik azzal a számmal, ahányszor \(\displaystyle a_{n-1}\) az \(\displaystyle a_{1}, a_{2}, \ldots, a_{n-1}\) sorozatban szerepel.
Bizonyítsuk be, hogy \(\displaystyle a_{1}, a_{3}, a_{5}, \ldots\) és \(\displaystyle a_{2}, a_{4}, a_{6}, \ldots\) sorozatok valamelyike egy idő után periodikus.
(A \(\displaystyle b_{1}, b_{2}, b_{3}, \ldots\) végtelen sorozat egy idő után periodikus, ha léteznek \(\displaystyle p\) és \(\displaystyle M\) pozitív egészek, melyekre \(\displaystyle b_{m+p}=b_{m}\) minden \(\displaystyle m \geq M\) esetén.)
|
| Előzmény: [375] Lpont, 2024-07-18 13:13:00 |
|
|
| [378] Lpont | 2024-07-24 13:41:48 |
 Köszönöm, ismerem az oldalt minden évben innen töltöm le az aktuális feladatokat, de most a 82MB méretű pdf-et többszöri tömörítés után sem sikerült 50MB alá vinnem, így maradt a másolás -> beillesztés, ami aztán a hibás szöveget okozta.
|
| Előzmény: [377] Ármós Lajos, 2024-07-24 11:11:07 |
|
|
| [376] Kós Géza | 2024-07-20 13:39:12 |
 Közben megszületett a végeredmény.
| 1 | 2 | 3 | 4 | 5 | 6 | össz. | hely | érem |
| Simon László Bence | 7 | 7 | 7 | 7 | 7 | 0 | 35 | 5–10 | aranyérem |
| Szakács Ábel | 7 | 7 | 2 | 7 | 7 | 0 | 30 | 29–46 | aranyérem |
| Czanik Pál | 7 | 2 | 1 | 7 | 7 | 1 | 25 | 90–99 | ezüstérem |
| Bodor Mátyás | 7 | 7 | 0 | 7 | 1 | 0 | 22 | 147–181 | ezüstérem |
| Varga Boldizsár | 7 | 7 | 0 | 7 | 1 | 0 | 22 | 147–181 | ezüstérem |
| Tarján Bernát | 7 | 7 | 6 | 1 | 0 | 0 | 21 | 182–215 | bronzérem |
| csapat | 42 | 37 | 16 | 36 | 23 | 1 | 155 | 8 | |
|
| Előzmény: [375] Lpont, 2024-07-18 13:13:00 |
|
|
| [374] Lpont | 2024-07-18 09:07:35 |
 Az idei IMO feladatok:
2024. július 16., kedd
1. feladat Határozzuk meg az összes α valós számot, amelyre minden pozitív egész n esetén teljesül, hogy n osztja a következő egész számot: ⌊α⌋ + ⌊2α⌋ + · · · + ⌊nα⌋. (A ⌊z⌋ a legnagyobb egész számot jelöli, amely kisebb vagy egyenlő, mint z. Például ⌊−π⌋ = −4 és ⌊2⌋ = ⌊2,9⌋ = 2.)
2. feladat Határozzuk meg az összes, pozitív egészekből álló (a, b) számpárt, melyre léteznek g és N pozitív egészek úgy, hogy lnko(a n + b, bn + a) = g teljesül minden n ⩾ N egészre. (Az x és y egész számok legnagyobb közös osztóját lnko(x, y) jelöli.)
3. feladat Legyen a1, a2, a3, . . . pozitív egészek egy végtelen sorozata, valamint legyen N egy pozitív egész. Tegyük fel, hogy minden n > N esetén an megegyezik azzal a számmal, ahányszor an−1 az a1, a2, . . . , an−1 sorozatban szerepel. Bizonyítsuk be, hogy a1, a3, a5, . . . és a2, a4, a6, . . . sorozatok valamelyike egy idő után periodikus. (A b1, b2, b3, . . . végtelen sorozat egy idő után periodikus, ha léteznek p és M pozitív egészek, melyekre bm+p = bm minden m ⩾ M esetén.)
2024. július 17., szerda
4. feladat Tegyük fel, hogy az ABC háromszögben AB < AC < BC. Jelölje ω az ABC háromszög beírt körét, I pedig ω középpontját. Legyen X a BC egyenes C-től különböző pontja úgy, hogy az Xen átmenő, AC-vel párhuzamos egyenes érinti ω-t. Továbbá legyen Y a BC egyenes B-től különböző pontja úgy, hogy az Y -on átmenő, AB-vel párhuzamos egyenes érinti ω-t. Messe az AI egyenes az ABC háromszög körülírt körét a P ̸= A pontban. Jelölje K és L az AC, illetve AB szakasz felezőpontját. Bizonyítsuk be, hogy KIL∢ + Y P X∢ = 180.
5. feladat Turbó, a csiga a következő játékot játssza egy 2024 sorból és 2023 oszlopból álló táblán, melynek 2022 mezőjén egy-egy szörny rejtőzik. Kezdetben Turbó nem ismeri a szörnyek helyét, de tudja, hogy az első és utolsó sort leszámítva minden sorban pontosan egy, valamint minden oszlopban legfeljebb egy szörny található. Turbó kísérleteket tesz arra, hogy eljusson az első sorból az utolsóba. Minden kísérlete során kiválasztja, hogy az első sor melyik mezőjéből indul, majd minden lépésében egy oldalszomszédos mezőre lép. (Visszatérhet olyan mezőre, melyen már járt.) Ha olyan mezőre lép, ahol szörny rejtőzik, akkor véget ér a kísérlete, visszakerül az első sorba, és új kísérletet kezd. A szörnyek nem változtatják a helyüket, és Turbó emlékszik, hogy az általa meglátogatott mezők közül melyeken volt szörny. Ha az utolsó sor bármelyik mezőjét eléri, akkor befejeződik a kísérlet, és a játék véget ér. Határozzuk meg azt a minimális n értéket, melyre Turbónak létezik olyan stratégiája, amellyel a szörnyek elhelyezkedésétől függetlenül biztosan eléri az utolsó sort legfeljebb n kísérlettel.
6. feladat Jelölje Q a racionális számok halmazát. Egy f : Q → Q függvényt pimasznak nevezünk, ha rendelkezik a következő tulajdonsággal: minden x, y ∈ Q esetén fennáll, hogy f(x + f(y)) = f(x) + y vagy f(f(x) + y) = x + f(y). Mutassuk meg, hogy létezik c egész szám úgy, hogy minden f pimasz függvényre legfeljebb c különböző racionális szám áll elő f(r) + f(−r) alakban, ahol r racionális szám; valamint határozzuk meg c legkisebb lehetséges értékét.
|
|
| [373] Ármós Lajos | 2023-11-14 18:39:15 |
 Régóta és többször is próbálkoztam a 2018/6-os feladatra egy elemi geometriai megoldást adni, míg végül is most sikerült. A megoldás a forgatva nyújtáson és egy geometriai egyenlőtlenségen alapul. Íme: https://rb.gy/av0yrc
|
|
| [372] Lpont | 2023-04-18 16:13:58 |
 Gratulálok az EGMO-n versenyző lányoknak és tanáraiknak a szép eredményhez!
https://www.egmo.org/registration/2023/person?@template=scoreboard
|
|






